
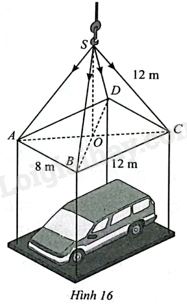
Tính độ lớn của các lực căng trên mỗi sợi dây cáp trong Hình 16. Cho biết khối lượng xe là 1900 kg, gia tốc là 10 m/s, khung nâng có khối lượng 100 kg và có dạng hình chóp \(S.ABCD\) với đáy \(ABCD\) là hình chữ nhật tâm \(O\), \(AB=8m,BC=12m,SC=12m\) và \(SO\) vuông góc với \(\left( {ABCD} \right)\). Làm tròn kết quả đến hàng đơn vị của Newton.

‒ Sử dụng định lý Pitago và lượng giác.
‒ Công thức tính độ lớn trọng lực: \(P = m.g\).
Advertisements (Quảng cáo)

\(\begin{array}{l}AC = B{\rm{D}} = \sqrt {A{B^2} + B{C^2}} = \sqrt {{8^2} + {{12}^2}} = 4\sqrt {13} \\OC = \frac{1}{2}AC = 2\sqrt {13} ;SO = \sqrt {S{C^2} - O{C^2}} = \sqrt {{{12}^2} - {{\left( {2\sqrt {13} } \right)}^2}} = 2\sqrt {23} \\\sin \widehat {SCO} = \frac{{SO}}{{SC}} = \frac{{2\sqrt {23} }}{{12}} = \frac{{\sqrt {23} }}{6}\end{array}\)
Gọi \(P\) là độ lớn của trọng lực xe và khung sắt nâng, \(F\) là độ lớn của lực căng trên mỗi sợi cáp.
Ta có \(P = \left( {1900 + 100} \right).10 = 20000\left( N \right)\)
\(F\sin \widehat {SCO} = \frac{P}{4} \Rightarrow F = \frac{P}{{4\sin \widehat {SCO}}} = \frac{{20000}}{{4.\frac{{\sqrt {23} }}{6}}} \approx 6255\left( N \right)\).
