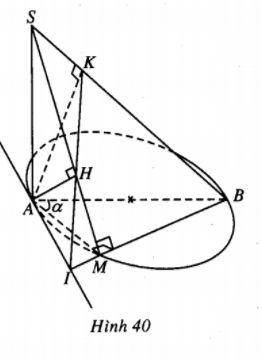
Cho đường tròn đường kính AB = 2R nằm trong mặt phẳng \(\left( P \right)\) và một điểm M nằm trên đường tròn đó sao cho \(\widehat {MAB} = \alpha \). Trên đường thẳng vuông góc với \(\left( P \right)\) tại A, lấy điểm S sao cho SA=h. Gọi H và K lần lượt là hình chiếu vuông góc của A trên SM và SB.
a) Chứng minh rằng \(SB \bot mp\left( {KHA} \right)\).
b) Gọi I là giao điểm của HK với \(\left( P \right)\). Hãy chứng minh AI là tiếp tuyến của đường tròn đã cho.
c) Cho h = 2R, \(\alpha = {30^0}\), tính thể tích khối chóp S.KHA.

(h.40)
a) Ta có \(BM \bot AM\) (vì M nằm trên đường tròn đường kính AB) và \(BM \bot SA\) (do \(SA \bot \left( P \right)\)), suy ra \(BM \bot \left( {SAM} \right) \Rightarrow BM \bot AH.\)
Mặt khác \(AH \bot SM,\) suy ra \(AH \bot SB,\)
Advertisements (Quảng cáo)
Theo giả thiết , ta lại có \(AK \bot SB\)
Vậy \(SB \bot \left( {KHA} \right).\)
b) Vì \(SB \bot \left( {KHA} \right)\) nên \(SB \bot AI\), mặt khác \(SA \bot AI\)nên \(AI \bot AB\), mà AI thuộc \(mp\left( P \right)\), suy ra AI là tiếp tuyến của đường tròn đã cho tại điểm A.
c) Cách 1. Ta có :
\(\eqalign{ & {{{V_{S.KHA}}} \over {{V_{S.BMA}}}} = {{SK} \over {SB}}.{{SH} \over {SM}} = {{SK.SB} \over {S{B^2}}}.{{SH.SM} \over {S{M^2}}} \cr&= {{S{A^4}} \over {S{B^2}.S{M^2}}} \cr & = {{(2R)^4} \over {\left( {4{R^2} + 4{R^2}} \right).\left( {4{R^2} + A{M^2}} \right)}} \cr&= {{2{R^2}} \over {4{R^2} + 4{R^2}.{{\cos }^2}\alpha }} = {1 \over {2\left( {1 + {{\cos }^2}\alpha } \right)}}, \cr & {V_{S.BMA}} = {1 \over 3}{S_{BMA}}.SA = {1 \over 6}AM.BM.SA \cr&= {1 \over 6}2R\cos \alpha .2Rsin\alpha .2R \cr & = {{2{R^3}} \over 3}\sin 2\alpha = {{2{R^3}} \over 3}.{{\sqrt 3 } \over 2} = {{{R^3}\sqrt 3 } \over 2}. \cr} \)
Vậy \({V_{S.KHA}} = {1 \over {2\left( {1 + {{\cos }^2}\alpha } \right)}}.{{{R^3}\sqrt 3 } \over 3} \)
\(= {1 \over {2\left( {1 + {3 \over 4}} \right)}}.{{{R^3}\sqrt 3 } \over 3} = {{2{R^3}\sqrt 3 } \over {21}}\)
Cách 2. Dễ thấy \({V_{S.KHA}} = {1 \over 3}{S_{KHA}}.SK.\)
Dùng hệ thức lượng trong tam giác vuông, ta có thể tính được SK, AH, AK, HK ( với chú ý rằng tam giác KHA vuông ở H) theo R. Từ đó tính được thể tích khối chóp S.KHA.
