Cho hình chóp S.ABC có \(SA \bot mp(ABC),AB = c,AC = b\) , \(\widehat {BAC} = \alpha \). Gọi B1, C1 lần lượt là hình chiếu vuông góc của A trên SB, SC. Chứng mình rằng các điểm A, B, C, B1,C1 cùng thuộc một mặt cầu và tính bán kính của mặt cầu đó theo b, c,\(\alpha \).

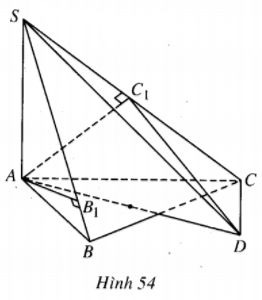
Gọi AD là đường kính của đường tròn ngoại tiếp tam giác ABC, khi đó \(CD \bot AC,\) mặt khác \(CD \bot SA\), từ đó \(CD \bot mp(SAC)\), vậy \(CD \bot A{C_1}\).
Theo giả thiết \(A{C_1} \bot SC\) nên \(A{C_1} \bot {C_1}D.\)
Tương tự như trên, ta cũng có \(\widehat {ABD} = {90^0},\widehat {A{B_1}D} = {90^0}.\)
Vậy AD là đường kính của mặt cầu đi qua các điểm A, B, C, B1, C1.
Advertisements (Quảng cáo)
Bán kính R của mặt cầu đó cũng là bán kính đường tròn ngoại tiếp tam giác ABC, do đó \({{BC} \over {\sin A}} = 2R,\) mặt khác
\(B{C^2} = A{B^2} + A{C^2} - 2AB.AC.{\mathop{\rm cosA}\nolimits} \) hay \(BC = \sqrt {{b^2} + {c^2} - 2bc.cos\alpha } ,\)
Vậy \(R = {{\sqrt {{b^2} + {c^2} - 2bc.cos\alpha } ,} \over {2\sin \alpha }}\)
Chú ý. Có thể chứng minh các điểm A, B, C, B1, C1 cùng thuộc một mặt cầu như sau :
Xét các tam giác vuông SAB, SAC, ta có \(S{A^2} = SB.S{B_1},S{A^2} = SC.S{C_1},\)từ đó \(SB.S{B_1} = SC.S{C_1},\) suy ra B, C, B1, C1 cùng thuộc một đường tròn.
Như vậy, hình chóp A.BCC1B1 có đáy BCC1B1 có đường tròn ngoại tiếp nên hình chóp đó có mặt cầu ngoại tiếp, tức là các điểm A, B, C, B1, C1 cùng thuộc một mặt cầu.
