Xét sự đồng biến, nghịch biến của các hàm số:
a) \(y = 3{x^2} - 8{x^3}\)
b) \(y = 16x + 2{x^2} - {{16} \over 3}{x^3} - {x^4}\)
c) \(y = {x^3} - 6{x^2} + 9x\)
d) \(y = {x^4} + 8{x^2} + 5\)
Hướng dẫn làm bài
a) TXĐ: R
\(y’ = 6x - 24{x^2} = 6x(1 - 4x)\)
y’ = 0 <=> \(\left[ {\matrix{{x = 0} \cr {x = {1 \over 4}} \cr} } \right.\)
y’ > 0 trên khoảng (0;\({1 \over 4}\) ) , suy ra y đồng biến trên khoảng (0;\({1 \over 4}\) )
y’ < 0 trên các khoảng (-∞;0 ); \(({1 \over 4}; + \infty )\), suy ra y nghịch biến trên các khoảng (-∞;0 ); \(({1 \over 4}; + \infty )\)
b) TXĐ: R
\(y’ = 16 + 4x - 16{x^2} - 4{x^3} = - 4(x + 4)({x^2} - 1)\)
y’ = 0 <=> \(\left[ {\matrix{{x = - 4} \cr {x = - 1} \cr {x = 1} \cr} } \right.\)
Advertisements (Quảng cáo)
Bảng biến thiên:
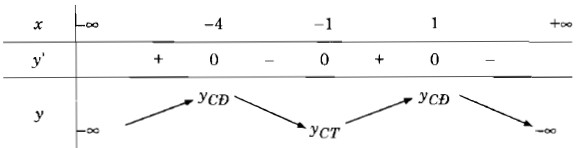
Vậy hàm số y đã cho đồng biến trên các khoảng (-∞; -4) và (-1; 1), nghịch biến trên các khoảng (-4; -1) và (1; +∞)
c) TXĐ: R
\(y’ = 3{x^2} - 12x + 9\)
y’=0 <=> \(\left[ {\matrix{{x = 1} \cr {x = 3} \cr} } \right.\)
y’ > 0 trên các khoảng (-∞; 1), (3; +∞) nên y đồng biến trên các khoảng (-∞; 1), (3; +∞)
y'< 0 trên khoảng (1; 3) nên y nghịch biến trên khoảng (1; 3)
d) TXĐ: R
\(y’ = 4{x^3} + 16 = 4x({x^2} + 4)\)
y’ = 0 <=> x = 0
y’ > 0 trên khoảng (0; +∞) => y đồng biến trên khoảng (0; +∞)
y’ < 0 trên khoảng (-∞; 0) => y nghịch biến trên khoảng (-∞; 0)
