Tìm cực trị của các hàm số sau:
a) \(y = - 2{x^2} + 7x - 5\)
b) \(y = {x^3} - 3{x^2} - 24x + 7\)
c) \(y = {x^4} - 5{x^2} + 4\)
d) \(y = {(x + 1)^3}(5 - x)\)
e) \(y = {(x + 2)^2}{(x - 3)^3}\)
Hướng dẫn làm bài:
a) \(y = - 2{x^2} + 7x - 5\) . TXĐ: R
\(\eqalign{
& y’ = - 4x + 7,y’ = 0 < = > x = {7 \over 4} \cr
& y” = - 4 = > y”({7 \over 4}) = - 4 < 0 \cr} \)
Vậy \(x = {7 \over 4}\) là điểm cực đại của hàm số và \({y_{CD}} = {9 \over 8}\)
b) \(y = {x^3} - 3{x^2} - 24x + 7\) . TXĐ: R
\(y’ = 3{x^2} - 6x - 24 = 3({x^2} - 2x - 8)\)
\(y’ = 0 \Leftrightarrow \left[ \matrix{
x = - 2 \hfill \cr
x = 4 \hfill \cr} \right.\)
Vì \(y”( - 2) = - 18 < 0,y”(4) = 18 > 0\) nên hàm số đạt cực đại tại x = - 2 ; đạt cực tiểu tại x = 4 và yCĐ = y(-2) = 35 ; yCT = y(4) = -73.
c) \(y = {x^4} - 5{x^2} + 4\)
TXĐ: R
\(\eqalign{
& = {{2{x^2} - 2{m^2} - {x^2} - 2mx + 3} \over {{{(x - m)}^2}}} = {{{x^2} - 2mx - 2{m^2} + 3} \over {{{(x - m)}^2}}} \cr
& y’ = 4{x^3} - 10x = 2x(2{x^2} - 5) \cr} \)
Advertisements (Quảng cáo)
$$y’ = 0 \Leftrightarrow \left[ \matrix{
x = 0 \hfill \cr
x = - \sqrt {{5 \over 2}} \hfill \cr
x = \sqrt {{5 \over 2}} \hfill \cr} \right.$$
Vì \(y”( \pm \sqrt {{5 \over 2}} ) = 20 > 0,y”(0) = - 10 < 0\)
Nên hàm số đạt cực đại tại x = 0, đạt cực tiểu tại \(x = \pm \sqrt {{5 \over 2}} \) và ta có:
yCĐ = y(0) = 4 , \({y_{_{CT}}} = y( \pm \sqrt {{5 \over 2}} ) = - {9 \over 4}\)
d) TXĐ: R
\(y’ = - {(x + 1)^3} + 3{(x + 1)^2}(5 - x) = 2{(x + 1)^2}(7 - 2x)\)
\(y’ = 0 \Leftrightarrow \left[ \matrix{
x = - 1 \hfill \cr
x = {7 \over 2} \hfill \cr} \right.\)
Bảng biến thiên:
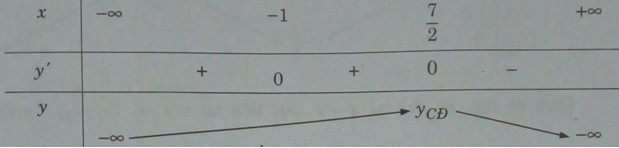
Hàm số đạt cực đại tại \(x = {7 \over 2};{y_{CD}} = y({7 \over 2}) = {{2187} \over {16}}\)
e) TXĐ: R
\(y’ = 2(x + 2){(x - 3)^3} + 3{(x + 2)^2}{(x - 3)^2} = 5x(x + 2){(x - 3)^2}\)
\(y’ = 0 \Leftrightarrow \left[ \matrix{
x = - 2 \hfill \cr
x = 0 \hfill \cr
x = 3 \hfill \cr} \right.\)
Bảng biến thiên:

Từ đó suy ra yCĐ = y(-2) = 0 ; yCT = y(0) = -108.
