Tìm các số thực p và q sao cho hàm số
\(f(x) = x + p + {q \over {x + 1}}\)
Đạt cực đại tại điểm \(x = - 2{\rm{ }}\) và \({\rm{ }}f\left( { - 2} \right) = - 2\).
Giải
Ta có
\(f'(x) = 1 - {q \over {{{\left( {x + 1} \right)}^2}}}\) với mọi \(x \ne - 1\)
- Nếu \(q \le 0\) thì \(f'(x) > 0\) với mọi \(x \ne - 1\). Do đó hàm số đồng biến trên mỗi khoảng \(\left( { - \infty ; - 1} \right)\) và \(\left( { - 1; + \infty } \right)\) . Hàm số không có cực đại, cực tiểu.
Advertisements (Quảng cáo)
- Nếu q > 0 thì phương trình
\(f'(x) = {{{x^2} + 2x + 1 - q} \over {{{\left( {x + 1} \right)}^2}}} = 0\)
Có hai nghiệm phân biệt \({x_1} = - 1 - \sqrt q \) và \({x_2} = - 1 + \sqrt q \)
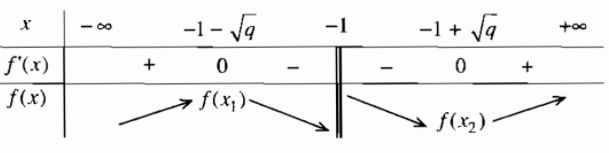
Hàm số đạt cực đại tại điểm \({x_1} = - 1 - \sqrt q \) và đạt cực tiểu tại điểm \({x_2} = - 1 + \sqrt q \). Hàm số đạt cực đại tại điểm x = -2 khi và chỉ khi
\( - 1 - \sqrt q = - 2 \Leftrightarrow \sqrt q = 1 \Leftrightarrow q = 1\)
\(f(-2) = - 2 \Leftrightarrow p = 1\)
