Tìm cực trị của các hàm số sau:
a) \(y = x - 6\root 3 \of {{x^2}} \)
b) \(y = (7 - x)\root 3 \of {x + 5}\)
c) \(y = {x \over {\sqrt {10 - {x^2}} }}\)
d) \(y = {{{x^3}} \over {\sqrt {{x^2} - 6} }}\)
Hướng dẫn làm bài:
a) TXĐ: R
\(y’ = 1 - {4 \over {\root 3 \of x }} = {{\root 3 \of x - 4} \over {\root 3 \of x }}\)
\(y’ = 0 < = > x = 64\)
Bảng biến thiên:
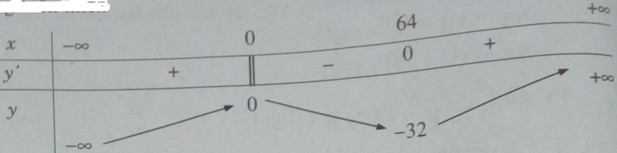
Vậy ta có yCĐ = y(0) = 0 và yCT = y(64) = -32.
b) Hàm số xác định trên khoảng \(( - \infty ; + \infty )\) .
Advertisements (Quảng cáo)
\(y’ = - \root 3 \of {x + 5} + {{7 - x} \over {3\root 3 \of {{{(x + 5)}^2}} }} = {{ - 4(x + 2)} \over {3\root 3 \of {{{(x + 5)}^2}} }}\)
Bảng biến thiên:
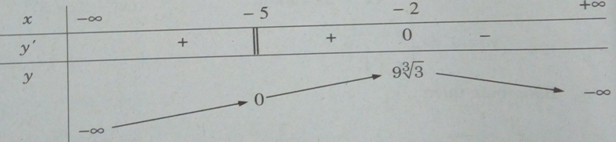
Vậy \({y_{CD}} = y( - 2) = 9\root 3 \of 3 \)
c) Hàm số xác định trên khoảng \(( - \sqrt {10} ;\sqrt {10} )\) .
\(y’ = {{\sqrt {10 - {x^2}} + {{{x^2}} \over {\sqrt {10 - {x^2}} }}} \over {10 - {x^2}}} = {{10} \over {(10 - {x^2})\sqrt {10 - {x^2}} }}\)
Vì y’ > 0 với mọi \(( - \sqrt {10} ;\sqrt {10} )\) nên hàm số đồng biến trên khoảng đó và do đó không có cực trị.
d) TXĐ: \(D = ( - \infty ; - \sqrt 6 ) \cup (\sqrt 6 ; + \infty )\)
\(\eqalign{
& y’ = {{3{x^2}\sqrt {{x^2} - 6} - {{{x^4}} \over {\sqrt {{x^2} - 6} }}} \over {{x^2} - 6}} \cr
& = {{3{x^2}({x^2} - 6) - {x^4}} \over {\sqrt {{{({x^2} - 6)}^3}} }} \cr
& = {{2{x^2}({x^2} - 9)} \over {\sqrt {{{({x^2} - 6)}^3}} }} \cr} \)
Bảng biến thiên:
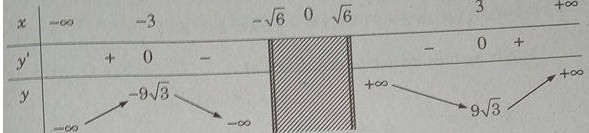
Từ đó ta thấy hàm số đạt cực đại tại x = -3, đạt cực tiểu tại x =- 3 và \({y_{CT}} = y(3) = 9\sqrt 3 ;{y_{CD}} = y( - 3) = - 9\sqrt 3 \)
