a) Cho hàm số \(y = {{3 - x} \over {x + 1}}\) có đồ thị (H)
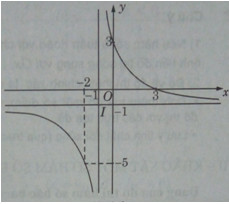
Chỉ ra một phép biến hình biến (H) thành (H’) có tiệm cận ngang y = 2 và tiệm cận đứng x = 2.
b) Lấy đối xứng (H’) qua gốc (O), ta được hình (H’’). Viết phương trình của (H’’).
Hướng dẫn làm bài:
Advertisements (Quảng cáo)
a) Từ đồ thị hàm số (H), để có hình (H’) nhận y = 2 là tiệm cận ngang và x = 2 là tiệm cận đứng, ta tịnh tiến đồ thị (H) song song với trục Oy lên trên 3 đơn vị, sau đó tịnh tiến song song với trục Ox về bên phải 3 đơn vị, ta được các hàm số tương ứng sau:
\(\eqalign{
& y = f(x) = {{3 - x} \over {x + 1}} + 3 = {{3 - x + 3x + 3} \over {x + 1}} = {{2x + 6} \over {x + 1}} \cr
& y = g(x) = {{2(x - 3) + 6} \over {x - 3 + 1}} = {{2x} \over {x - 2}} \cr} \)
b) Lấy đối xứng hình (H’) qua gốc O, ta được hình (H’’) có phương trình là:
\(y = h(x) = - {{2( - x)} \over {( - x) - 2}} = - {{ - 2x} \over { - 2 - x}} = - {{2x} \over {x + 2}}\).
