Chứng minh rằng phương trình sau không thể có hai nghiệm thực trong đoạn [0; 1].. Bài 1.9 trang 9 Sách bài tập (SBT) Giải tích 12 - Bài 1. Sự đồng biến nghịch biến của hàm số
Chứng minh rằng phương trình \({x^3} - 3x + c = 0\) không thể có hai nghiệm thực trong đoạn [0; 1].
Hướng dẫn làm bài:
Đặt \(f(x) = {x^3} - 3x + C\) . TXĐ: R
\(f'(x) = 3{x^2} - 3 = 3({x^2} - 1)\)
Advertisements (Quảng cáo)
\(f'(x) = 0 \Leftrightarrow \left[ \matrix{
x = 1 \hfill \cr
x = - 1 \hfill \cr} \right.\)
Bảng biến thiên:
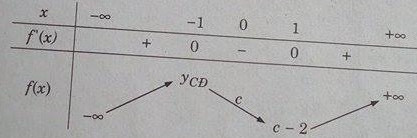
Trên đoạn [0; 1] hàm số f(x) nghịch biến nên đồ thị của hàm số f(x) không thể cắt trục hoành tại hai điểm trên đoạn này, tứclà phương trình x3 – 3x + C = 0 không thể có hai nghiệm thực trên đoạn [0; 1].
