Hình chóp tam giác S.ABC có SA = SB = SC = a và có chiều cao bằng h. Xác định tâm và bán kính của mặt cầu ngoại tiếp hình chóp. Tính diện tích của mặt cầu đó.
Hướng dẫn làm bài:
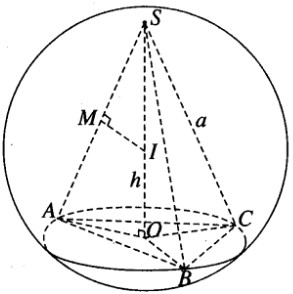
Giả sử ta có mặt cầu tâm I đi qua các đỉnh S, A, B, C của hình chóp. Mặt phẳng (ABC) cắt mặt cầu ngoại tiếp hình chóp theo giao tuyến là đường tròn tâm O ngoại tiếp tam giác ABC. Vì SA = SB = SC nên ta có \(SO \bot (ABC)\) và OS là trục của đường tròn tâm O. Do đó \(SO \bot AO\) . Trong tam giác SAO, đường trung trực của đoạn SA cắt SO tại I và ta được hai tam giác vuông đồng dạng là SIM và SAO, với M là trung điểm của cạnh SA.
Advertisements (Quảng cáo)
Ta có \({{SI} \over {SA}} = {{SM} \over {SO}} = {{SA} \over {2SO}}\) với SI = IA = IB = IC = r
Vậy \(r = SI = {{S{A^2}} \over {2SO}} = {{{a^2}} \over {2h}}\)
Do đó diện tích của mặt cầu ngoại tiếp hình chóp S.ABC đã cho là :
\(S = 4\pi {r^2} = 4\pi {({{{a^2}} \over {2h}})^2} = \pi {{{a^4}} \over {{h^2}}}\)
