Cho hình cầu tâm O bán kính r. Lấy một điểm A trên mặt cầu và gọi \((\alpha )\) là mặt phẳng đi qua A sao cho góc giữa OA và \((\alpha )\) bằng 300.
a) Tính diện tích của thiết diện tạo bởi \((\alpha )\) và hình cầu.
b) Đường thẳng đi qua A vuông góc với mặt phẳng \((\alpha )\) cắt mặt cầu tại B. Tính độ dài đoạn AB.
Hướng dẫn làm bài:
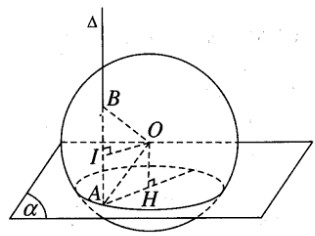
a) Gọi H là hình chiếu vuông góc của tâm O trên mặt phẳng \((\alpha )\) . Theo giả thiết ta có \(\widehat {OAH} = {30^0}\) .
Advertisements (Quảng cáo)
Do đó: \(HA = OA.\cos {30^0} = r{{\sqrt 3 } \over 2}\)
Vậy diện tích của thiết diện tạo bởi \((\alpha )\) và hình cầu là: \(S = \pi .H{A^2} = {{3\pi {r^2}} \over 4}\)
b) Mặt phẳng (ABO) qua tâm O của hình cầu nên cắt mặt cầu theo đường tròn lớn qua A và B. Gọi I là trung điểm của đoạn AB ta có \(OI \bot AB\) . Vì AB // OH nên AIOH là hình chữ nhật.
Do đó \(AI = OH = {{OA} \over 2} = {r \over 2}\) . Vậy AB = 2AI = r
Chú ý: Có thể nhận xét rằng tam giác OAB cân tại O (OA = OB) và có góc \(\widehat {OAB} = {60^0}\) nên OAB là tam giác đều và suy ra AB = OA = OB = r.
