Advertisements (Quảng cáo)
Tính diện tich các hình phẳng giới hạn bởi các đường sau:
a) \(y = x – 1 + {{\ln x} \over x},y = x – 1\) và x = e;
b) y = x3 – x2 và \(y = {1 \over 9}(x – 1)\);
c) \(y = 1 – \sqrt {1 – {x^2}} \) và y = x2
Hướng dẫn làm bài
a) \({1 \over 2}\)
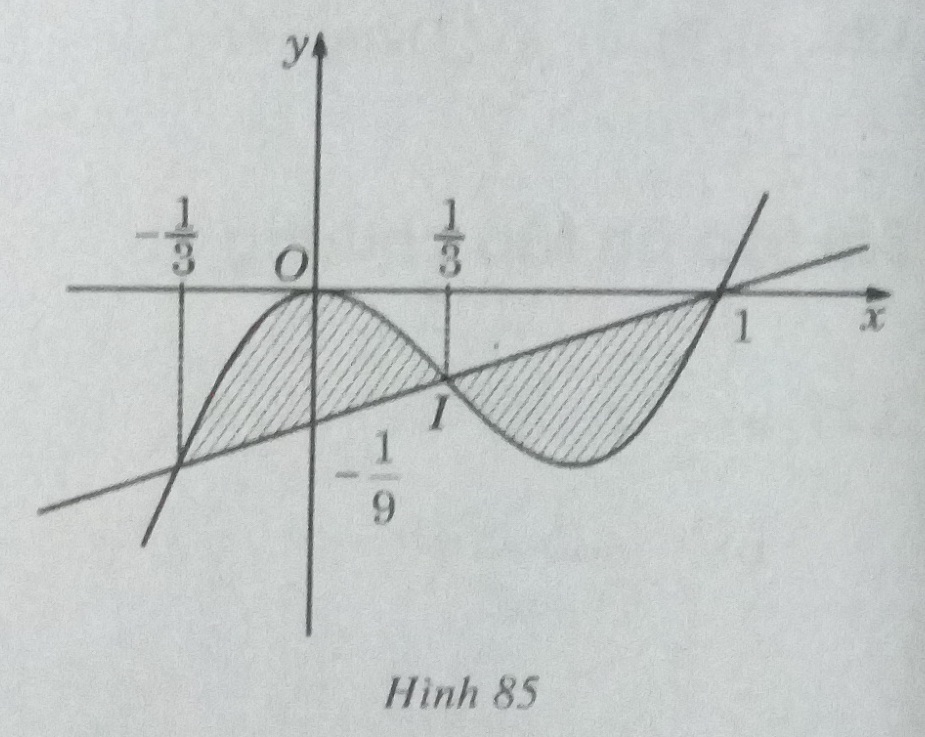
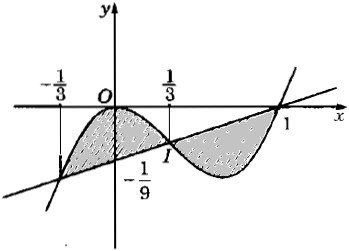
b) \({8 \over {81}}\) . HD: Đường thẳng \(y = {1 \over 9}(x – 1)\) đi qua tâm đối xứng \(I({1 \over 3}; – {2 \over {27}})\) của hàm số y = x3 – x2 .
Do đó, hình phẳng giới hạn bởi hai đường đã cho gồm hai hình vẽ đối xứng nhau qua điểm I (hình 85).
Advertisements (Quảng cáo)
Vậy : \(S = 2\int\limits_{ – {1 \over 3}}^{{1 \over 3}} {{\rm{[}}({x^3} – {x^2}) – {1 \over 9}(x – 1){\rm{]}}dx}\)
\( = 4\int\limits_0^{{1 \over 3}} {({1 \over 9} – {x^2})dx = {8 \over {81}}} \)
(theo bài 3.14. \(\int\limits_{ – {1 \over 3}}^{{1 \over 3}} {({x^3} – {1 \over 9}x)dx = 0} \))
c) \({\pi \over 2} – {4 \over 3}\)