Advertisements (Quảng cáo)
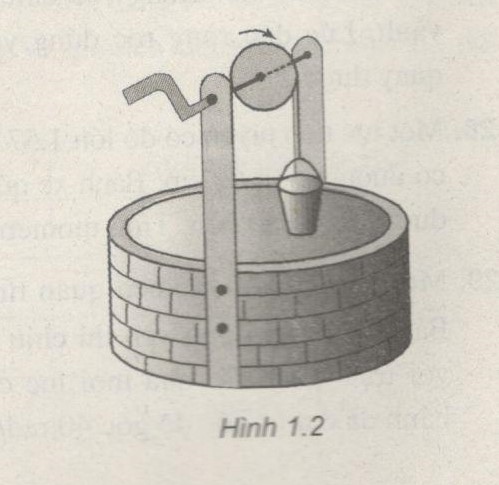
Một ròng rọc hình trụ, khối lượng M = 3kg, bán kính R = 0,4 m, được dùng để kéo nước trong một cái giếng (Hình 1.2). Một chiếc xô, khối lượng m = 2kg, được buộc vào một sợi dây quấn quanh ròng rọc. Nếu xô được thả từ miệng giếng thì sau 3 s nó chạm vào nước. Bỏ qua ma sát ở trục quay và momen quán tính của tay quay. Lấy \(g = 9,8\,m/{s^2}\). Tính :
a) Lực căng T và gia tốc của xô, biết dây không trượt trên ròng rọc
b) Độ sâu tính từ miệng giếng đến mặt nước.
Giải
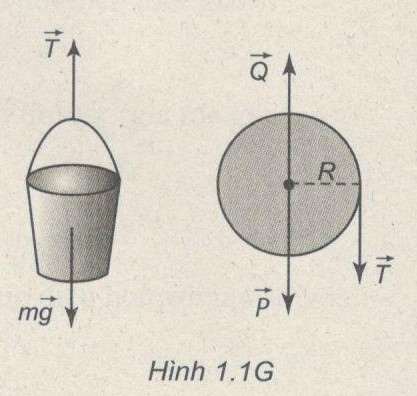
a) Đối với xô :
\(mg – T = ma\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left( 1 \right)\)
Đối với ròng rọc :
Advertisements (Quảng cáo)
\(T.R = I\gamma = {1 \over 2}M.{R^2}{{{a_t}} \over R} \Rightarrow T = {1 \over 2}M{a_t}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left( 2 \right)\)
Dây không trượt trên ròng rọc :
\({a_t} = a\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left( 3 \right)\)
Từ (1), (2), và (3) ta tính được : \(a = 5,60\,\,m/{s^2};T = 8,40\,\,N\)
b) \(h = {1 \over 2}a{t^2} = {1 \over 2}\left( {5,60} \right).{\left( 3 \right)^2} = 25,2\,\,m\)