Advertisements (Quảng cáo)
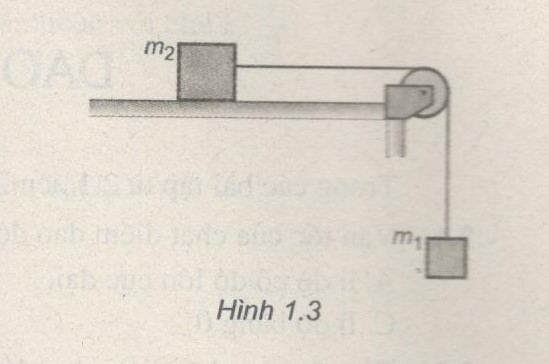
Hai vật có khổi lượng \({m_1} = 0,5\,\,kg\) và \({m_2} = 1,5\,\,kg\) được nối với nhau bằng một sợ dây nhẹ, không dãn, vắt qua một ròng rọc có trục quay nằm ngang và gắn cố định vào mép bàn (Hình 1.3). Ròng rọc có momen quán tính \(0,03\,kg.{m^2}\)và bán kính 10 cm. Coi rằng dây không trượt trên ròng rọc khi quay. Bỏ qua mọi ma sát.
a) Xác định gia tốc \({m_1}\) và \({m_2}\)
b) Tính độ dịch chuyển của \({m_2}\) trên mặt bàn sau 0,4 s kể từ lúc nó bắt đầu chuyển động.
Giải
a)
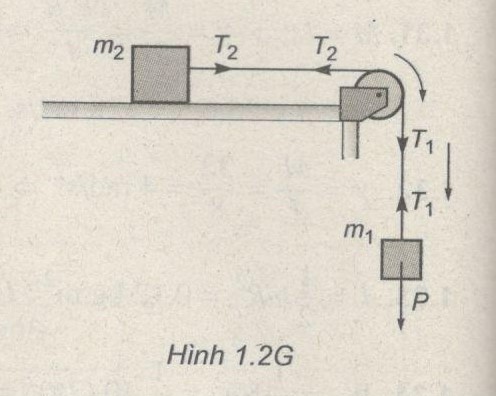
+) Xét vật 1 :
\({m_1}g – {T_1} = {m_1}a \Rightarrow {T_1} = {m_1}\left( {g – a} \right)\,\,\,\,\,\,\,\left( 1 \right)\)
+) Xét vật 2 :
\({T_2} = {m_2}a\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left( 2 \right)\)
+) Xét ròng rọc :
\(\left( {{T_1} – {T_2}} \right)R = I\gamma \Rightarrow {T_1} – {T_2} = I{a \over {{R^2}}}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left( 3 \right)\)
Từ (1) , (2) và (3), suy ra :
\(a = {{{m_1}g} \over {{m_1} + {m_2} + {I \over {{R^2}}}}}\)
Thay số, ta được : \(a = 0,98\,\,m/{s^2}\)
b) Độ dịch chuyển : \(s = {1 \over 2}a{t^2} = {1 \over 2}0,98.0,{4^2} = 0,0784\,m = 7,84\,cm\)