
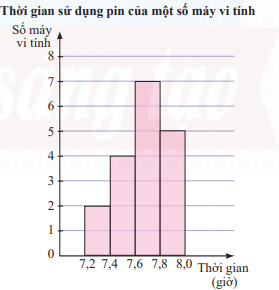
Kết quả khảo sát thời gian sử dụng liên tục (đơn vị: giờ) từ lúc sạc đầy cho đến khi hết của pin một số máy vi tính cùng loại được mô tả bằng biểu đồ bên. a) Hãy cho biết có bao nhiêu máy vi tính có thời gian sử dụng pin từ 7,2 đến dưới 7,4 giờ? b) Hãy xác định số trung bình và độ lệch chuẩn của thời gian sử dụng pin.

a) Quan sát đồ thị
b) Tính giá trị đại diện
Phương sai của mẫu số liệu ghép nhóm, kí hiệu \({S^2}\), được tính bởi công thức:
\({S^2} = \frac{1}{n}[{n_1}{({c_1} - \overline x )^2} + {n_2}{({c_2} - \overline x )^2} + ... + {n_k}{({c_k} - \overline x )^2}]\)
Trong đó: \(n = {n_1} + {n_2} + ... + {n_k}\) là cỡ mẫu
Advertisements (Quảng cáo)
\(\overline x = \frac{1}{n}({n_1}{c_1} + {n_2}{c_2} + ... + {n_k}{c_k})\) là số trung bình
Độ lệch chuẩn của mẫu số liệu ghép nhóm, kí hiệu \(S\), là căn bậc hai số học của phương sai.

a) Có 2 máy vi tính có thời gian sử dụng pin từ 7,2 đến dưới 7,4 giờ
b)
Cỡ mẫu: n = 18
Số trung bình: \(\overline x = \frac{{2.7,3 + 4.7,5 + 7.7,7 + 5.7,9}}{{18}} \approx 7,67\)
Phương sai: \({S^2} = \frac{{2.7,{3^2} + 4.7,{5^2} + 7.7,{7^2} + 5.7,{9^2}}}{{18}} - 7,{67^2} \approx 0,04\)
Độ lệch chuẩn: \(\sigma = \sqrt {0,04} \approx 0,19\)
