
Giá trị nhỏ nhất của hàm số \(y = \sqrt {{x^2} + 2x + 3} \) trên đoạn [–2; 3] là
A. \(\sqrt 3 \) B. \(\sqrt {30} \) C. \(\sqrt 2 \) D. 0

Cho hàm số y = f(x) xác định trên tập hợp D.
- Số M được gọi là giá trị lớn nhất của hàm số y = f(x) trên D nếu f(x) \( \le \) M với mọi x thuộc D và tồn tại \({x_0}\) thuộc D sao cho f(\({x_0}\)) = M. Kí hiệu M = \(\mathop {\max }\limits_D \)f(x).
- Số m được gọi là giá trị nhỏ nhất của hàm số y = f(x) trên D nếu f(x) \( \ge \) m với mọi x thuộc D và tồn tại \({x_0}\) thuộc D sao cho f(\({x_0}\)) = m. Kí hiệu m = \(\mathop {\min }\limits_D \)f(x).
Advertisements (Quảng cáo)

Chọn C
Tập xác định: \(D = \mathbb{R}\)
\(y’ = \frac{{x + 1}}{{\sqrt {{x^2} + 2x + 3} }} = 0 \Leftrightarrow x = - 1\)
Bảng biến thiên:
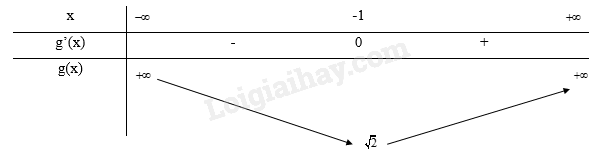
Từ bảng biến thiên ta thấy, \(\mathop {\min }\limits_D y = y( - 1) = \sqrt 2 \)
