Bài 17. Tính thể tích của khối hộp \(ABCD.A’B’C’D’\), biết rằng \(AA’B’D’\) là khối tứ diện đều cạnh \(a\).

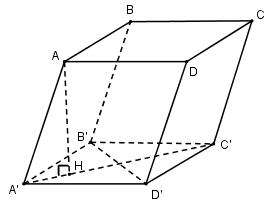
\(AA’B’D’\) là tứ diện đều nên đường cao \(AH\) có \(H\) là tâm của tam giác đều \(A’B’D’\) cạnh \(a\) do đó”
Advertisements (Quảng cáo)
\(\eqalign{
& A’H = {2 \over 3}A’O’ = {2 \over 3}{{a\sqrt 3 } \over 2} = {{a\sqrt 3 } \over 3} \cr
& \Rightarrow A{H^2} = AA{‘^2} - A'{H^2} = {a^2} - {{{a^2}} \over 3} = {{2{a^2}} \over 3} \cr
& \Rightarrow AH = a\sqrt {{2 \over 3}} = {{a\sqrt 6 } \over 3} \cr} \)
Diện tích tam giác đều \(A’B’D’\): \({S_{A’B’D’}} = {{{a^2}\sqrt 3 } \over 4}\)
Diện tích hình thoi \(A’B’C’D’\): \({S_{A’B’C’D’}} = 2{S_{B’C’D’}} = {{{a^2}\sqrt 3 } \over 2}\)
Vậy thể tích khối hộp đã cho là \(V = B.h = {{{a^2}\sqrt 3 } \over 2}.{{a\sqrt 6 } \over 3} = {{{a^3}\sqrt 2 } \over 2}\)
