Cho hình chóp tam giác S.ABC và M là một điểm nằm trong tam giác ABC. Các đường thẳng qua M song song với SA, SB, SC lần lượt cắt các mặt \(\left( {BCS} \right),\left( {CAS} \right),\left( {ABS} \right)\) tại A’, B’, C’. Chứng minh rằng :
a)\({{{V_{M.BCS}}} \over {{V_{S.ABC}}}} = {{MA’} \over {SA}};\)
b)\({{MA’} \over {SA}} + {{MB’} \over {SB}} + {{MC’} \over {SC}}\) không đổi. Tìm tổng đó.

(h.37)
a) Gọi N là giao điểm của MA và BC. Khi đó S, A’, N thẳng hàng vì chúng cùng nằm trên giao tuyến của hai mặt phẳng \(\left( {SBC} \right)\) và \(\left( {SA,A’M} \right)\).
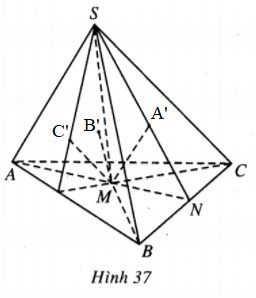
Gọi MM1 và AA1 là các đường vuông góc hạ từ M và A xuống \(mp\left( {SBC} \right)\) thì :
Advertisements (Quảng cáo)
\({{M{M_1}} \over {A{A_1}}} = {{MN} \over {AN}} = {{MA’} \over {SA}}.\)
Vậy \({{{V_{M.BCS}}} \over {{V_{S.ABC}}}} = {{{V_{M.BCS}}} \over {{V_{A.BCS}}}} = {{{1 \over 3}{S_{BCS}}.M{M_1}} \over {{1 \over 3}{S_{BCS}}A{A_1}}} = {{M{M_1}} \over {A{A_1}}} = {{MA’} \over {SA}}\)
b) Chứng minh tương tự như câu a), ta có :
\({{{V_{M.CAS}}} \over {{V_{S.ABC}}}} = {{MB’} \over {SB}},{{{V_{M.ABS}}} \over {{V_{S.ABC}}}} = {{MC’} \over {SC}}.\)
Vậy :
\({{MA’} \over {SA}} + {{MB’} \over {SB}} + {{MC’} \over {SC}} = {{{V_{M.BCS}} + {V_{M.CAS}} + {V_{M.ABS}}} \over {{V_{S.ABC}}}} \)
\(= {{{V_{S.ABC}}} \over {{V_{S.ABC}}}} = 1.\)
