Bài 54 trang 12 SBT Hình học lớp 12 Nâng Cao: Hình chóp S.ABCD có đáy ABCD...

Hình chóp S.ABCD có đáy ABCD là hình bình hành. Một mặt phẳng $\left( P \right)$ cắt SA, SB, SC, SD theo thứ tự tại K, L, M, N.

Chứng minh rằng :

$a){V_{S.ABC}} = {V_{S.ACD}} = {V_{S.ABD}} = {V_{S.BCD}};$

$b){{SA} \over {SK}} + {{SC} \over {SM}} = {{SB} \over {SL}} + {{SD} \over {SN}}.$

(h.38)

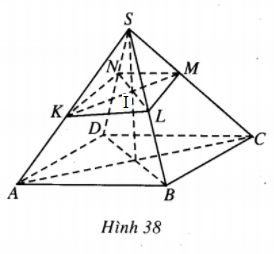
a) Dễ thấy các tam giác ABC, ACD, ABD, BCD đều có diện tích bằng nhau và bằng nửa diện tích S của hình bình hành ABCD ; các hình chóp S.ABC, S.ACD, S.ABD, S.BCD có chiều cao bằng nhau và bằng chiều cao h của hình chóp S.ABCD. Vậy

$\eqalign{  & {V_{S.ABC}} = {V_{S.ACD}} = {V_{S.ABD}} = {V_{S.BCD}}  \cr  &  = {{{V_{S.ABCD}}} \over 2} = {V \over 2}. \cr}$

b) Ta có :

$\eqalign{  & {{{V_{S.KLM}}} \over {{V \over 2}}} = {{SK} \over {SA}}.{{SL} \over {SB}}.{{SM} \over {SC}},\cr&{{{V_{S.KMN}}} \over {{V \over 2}}} = {{SK} \over {SA}}.{{SM} \over {SC}}.{{SN} \over {SD}}  \cr  &   \cr}$

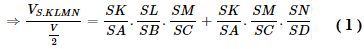
Tương tự

${{{V_{S.KLMN}}} \over {{V \over 2}}} = {{SL} \over {SB}}.{{SM} \over {SC}}.{{SN} \over {SD}} + {{SL} \over {SB}}.{{SN} \over {SD}}.{{SK} \over {SA}}\;\;\;\;(2)$

Từ (1) và (2) suy ra

${{SK} \over {SA}}.{{SL} \over {SB}}.{{SM} \over {SC}} + {{SK} \over {SA}}.{{SM} \over {SC}}.{{SN} \over {SD}}$

$= {{SL} \over {SB}}.{{SM} \over {SC}}.{{SN} \over {SD}} + {{SL} \over {SB}}.{{SN} \over {SD}}.{{SK} \over {SA}}.$

Nhân hai vế với ${{SA} \over {SK}}.{{SB} \over {SL}}.{{SC} \over {SM}}.{{SD} \over {SN}},$ ta được đẳng thức phải chứng minh.