hình tứ diện là một số không phụ thuộc vào vị trí của điểm M. Tổng đó bằng bao nhiêu nếu cạnh của tứ diện đều
bằng a ?. Bài 21 trang 28 SGK Hình học 12 Nâng cao – Bài 4. Thể tích của khối đa diện
Bài 21. Cho điểm \(M\) nằm trong hình tứ diện đều \(ABCD\). Chứng minh rằng tổng các khoảng cách từ \(M\) tới bốn mặt của hình tứ diện là một số không phụ thuộc vào vị trí của điểm \(M\). Tổng đó bằng bao nhiêu nếu cạnh của tứ diện đều bằng \(a\) ?
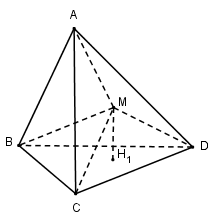
Gọi \({H_1},{H_2},{H_3},{H_4}\) lần lượt là hình chiếu của điểm M trên các mặt phẳng \((BCD) , (ACD) , (ABD) , (ABC)\).
Khi đó \(M{H_1},M{H_2},M{H_3},M{H_4}\) lần lượt là khoảng cách từ điểm \(M\) tới các mặt phẳng đó. Các mặt bên của tứ diện đều có cùng diện tích, ta kí hiệu các diện tích đó là \(S\) và gọi \(h\) là chiều cao của tứ diện đều. Ta có:
\(\eqalign{
& {V_{MBCD}} + {V_{MACD}} + {V_{MABD}} + {V_{MABC}} = {V_{ABCD}} \cr
& \Leftrightarrow {1 \over 3}S.M{H_1} + {1 \over 3}S.M{H_2} + {1 \over 3}S.M{H_3} + {1 \over 3}S.M{H_4} = {1 \over 3}S.h \cr
& \Leftrightarrow M{H_1} + M{H_2} + M{H_3} + M{H_4} = h \cr} \)
Vậy tổng các khoảng cách từ điểm \(M\) tới bốn mặt của tứ diện đều không phụ thuộc vào vị trí của điểm \(M\) nằm trong tứ diện đó.
Nếu tứ diện đều có cạnh bằng \(a\), ta tính \(h\).
Gọi \(H\) là trực tâm tam giác đều \(BCD\) và \(M\) là trung điểm của \(CD\).
Ta có:
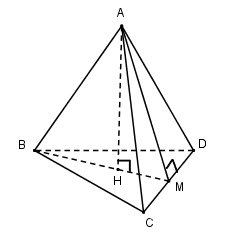
Advertisements (Quảng cáo)
\(\eqalign{
& {h^2} = A{H^2} = A{M^2} – H{M^2} = {\left( {{{a\sqrt 3 } \over 2}} \right)^2} – {\left( {{1 \over 3}.{{a\sqrt 3 } \over 2}} \right)^2} \cr
& \,\,\,\,\,\, = {{3{a^2}} \over 4} – {{{a^2}} \over {12}} = {{2{a^3}} \over 3} \Rightarrow h = {{a\sqrt 6 } \over 3} \cr} \)
Tổng khoảng cách nói trên bằng \({{a\sqrt 6 } \over 3}\).