Bài 31. Cho các số phức \({\rm{w}}= {{\sqrt 2 } \over 2}\left( {1 + i} \right)\) và \(\varepsilon = {1 \over 2}\left( { - 1 + i\sqrt 3 } \right)\)
a) Chứng minh rằng \({z_o} = \cos {\pi \over {12}} + i\sin {\pi \over {12}},\,{z_1} = {z_o}\varepsilon ,\,{z_2} = {z_o}{\varepsilon ^2}\) là các nghiệm của phương trình \({z^3} - {\rm{w}} = 0;\)
b) Biểu diễn hình học các số phức \({z_o},\,{z_1},\,{z_2}\)

a) Ta có: \({\rm{w}} = \cos {\pi \over 4} + i\sin {\pi \over 4}\)
Advertisements (Quảng cáo)
\(\eqalign{ & \varepsilon = \cos {{2\pi } \over 3} + i\sin {{2\pi } \over 3} \cr & z_o^3 = {\left( {\cos {\pi \over {12}} + i\sin {\pi \over {12}}} \right)^3} = \cos {\pi \over 4} + i\sin {\pi \over 4} ={\rm{w}} \cr & z_1^3 = {\left( {{z_o}\varepsilon } \right)^3} = z_o^3.{\varepsilon ^3} = {\rm{w}} \,\,\left( {\text{vì}\,\,\,{\varepsilon ^3} = 1} \right), \cr & z_2^3 = {\left( {z_o{\varepsilon ^2}} \right)^3} = z_o^3{\varepsilon ^6} = z_o^3 ={\rm{w}}\cr} \)
b) Biểu diễn: Các điểm A, B, C lần lượt biểu diễn \({z_0},\,\,{z_1},\,\,{z_2}\)
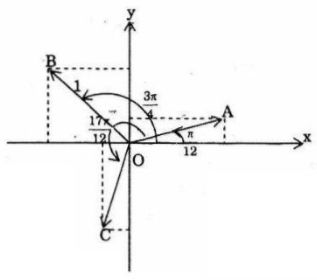
Nhận xét: A,B,C tạo thành một tam giác đều.
