Bài 50. Tính các tích phân sau:
\(a)\,\int\limits_0^{{\pi \over 2}} {{x^2}\sin 2xdx;} \) \(b)\,\int\limits_1^2 {x\left( {2{x^2} + 1} \right)} dx;\)
\(c)\,\int\limits_2^3 {\left( {x - 1} \right)} {e^{{x^2} - 2x}}dx.\)

a) Đặt
\(\left\{ \matrix{
u = {x^2} \hfill \cr
dv = \sin 2xdx \hfill \cr} \right. \Rightarrow \left\{ \matrix{
du = 2xdx \hfill \cr
v = - {1 \over 2}\cos 2x \hfill \cr} \right.\)
Do đó \(\int\limits_0^{{\pi \over 2}} {{x^2}\sin 2xdx} = \left. { - {1 \over 2}{x^2}\cos 2x} \right|_0^{{\pi \over 2}} + \int\limits_0^{{\pi \over 2}} {{x^2}\cos 2xdx} \)
\( = {{{\pi ^2}} \over 8} + \int\limits_0^{{\pi \over 2}} {x\cos 2xdx\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left( 1 \right)} \)
Đặt
\(\left\{ \matrix{
u = x \hfill \cr
dv = \cos 2xdx \hfill \cr} \right. \Rightarrow \left\{ \matrix{
du = dx \hfill \cr
v = {1 \over 2}\sin 2x \hfill \cr} \right.\)
Advertisements (Quảng cáo)
Do đó \(\int\limits_0^{{\pi \over 2}} {x\cos 2xdx\, = \left. {{1 \over 2}x\sin 2x} \right|_0^{{\pi \over 2}}} - {1 \over 2}\int\limits_0^{{\pi \over 2}} {\sin 2xdx} = \left. {{1 \over 4}\cos 2x} \right|_0^{{\pi \over 2}} = - {1 \over 2}\,\,\,\,\,\,\,\,\left( 2 \right)\)
Thay (2) vào (1) ta được: \(\int\limits_0^{{\pi \over 2}} {{x^2}\sin 2xdx = {{{\pi ^2}} \over 8}} - {1 \over 2}.\)
b) Đặt \(u = 2{x^2} + 1 \Rightarrow du = 4xdx \Rightarrow xdx = {{du} \over 4}\)
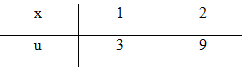
\(\int\limits_1^2 {x\left( {2{x^2} + 1} \right)dx = {1 \over 4}} \int\limits_3^9 {udu} = \left. {{1 \over 8}{u^2}} \right|_3^9 = 9\)
c) Đặt \(u = {x^2} - 2x \Rightarrow du = 2\left( {x - 1} \right)dx \Rightarrow \left( {x - 1} \right)dx = {{du} \over 2}\)
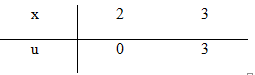
\(\int\limits_2^3 {\left( {x - 1} \right)} {e^{{x^2} - 2x}}dx = {1 \over 2}\int\limits_0^3 {{e^u}du = } \left. {{1 \over 2}{e^u}} \right|_0^3 = {1 \over 2}\left( {{e^3} - 1} \right).\)
