Bài 51.Tính diện tích các hình phẳng giới hạn bởi:
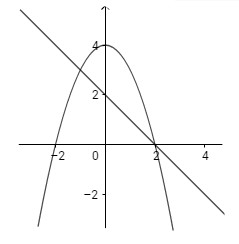
a) Đồ thị các hàm số \(y = 4 - {x^2},y = - x + 2;\)
b) Các đường cong có phương trình \(x = 4 - 4{y^2}\) và \(x = 1 - {y^4}\) trong miền \(x\ge0\).

a) Phương trình hoành độ giao điểm của hai đồ thị là:
\(4 - {x^2} = - x + 2 \Leftrightarrow {x^2} - x - 2 = 0 \Leftrightarrow \left[ \matrix{
x = - 1 \hfill \cr
x = 2 \hfill \cr} \right.\)
Advertisements (Quảng cáo)
Do đó
\(\eqalign{
& S = \int\limits_{ - 1}^2 {\left| {4 - {x^2} - \left( { - x + 2} \right)} \right|} dx = \int\limits_{ - 1}^2 {\left| { - {x^2} + x + 2} \right|} dx \cr
& \,\,\, = \int\limits_{ - 1}^2 {\left( { - {x^2} + x + 2} \right)} dx = \left. {\left( { - {{{x^3}} \over 3} + {{{x^2}} \over 2} + 2x} \right)} \right|_{ - 1}^2 = {9 \over 2} \cr} \)
b) Phương trình tung độ giao điểm của hai đồ thị là
\(4 - 4{y^2} = 1 - {y^4} \Leftrightarrow {y^4} - 4{y^2} + 3 = 0 \Leftrightarrow \left[ \matrix{
{y^2} = 1 \hfill \cr
{y^2} = 3 \hfill \cr} \right. \Leftrightarrow \left[ \matrix{
y = \pm 1 \hfill \cr
y = \pm \sqrt 3\; (\text{ loại vì } x<0)\hfill \cr} \right.\)
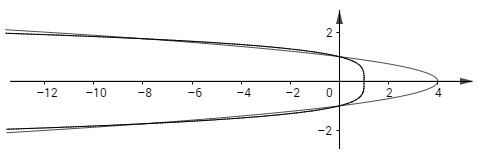
Diện tích giới hạn hai đồ thị ở phần \(x \ge 0\) là:
\(\eqalign{
& S = \int\limits_{ - 1}^1 {\left[ {4 - 4{y^2} - \left( {1 - {y^4}} \right)} \right]} dy \cr
& \,\,\, = \int\limits_{ - 1}^1 {\left( {{y^4} - 4{y^2} + 3} \right)} dy \cr
& \,\, = \left. {\left( {{{{y^5}} \over 5} - {4 \over 3}{y^3} + 3y} \right)} \right|_{ - 1}^1 = 2.{{28} \over {15}} = {{56} \over {15}} \cr} \)
