b) Với các giá trị nào t=của m đường thẳng y = m – x cắt đồ thị hàm số đã cho tại hao điểm phân biệt?
c) Gọi A và B là hai giao điểm đó. Tìm tập hợp các trung điểm của đoạn thẳng AB khi m biến thiên.. Bài 65 trang 58 sách giải tích 12 nâng cao - Bài 8. Một số bài toán thường gặp về đồ thị
Bài 65
a) Khảo sát sự biến thiên và vẽ đồ thị của hàm số: \(y = {{2{x^2} - x + 1} \over {x - 1}}\)
b) Với các giá trị nào t=của m đường thẳng \(y = m – x\) cắt đồ thị hàm số đã cho tại hao điểm phân biệt?
c) Gọi \(A\) và \(B\) là hai giao điểm đó. Tìm tập hợp các trung điểm của đoạn thẳng \(AB\) khi \(m\) biến thiên.

a) Tập xác định: \(D = \mathbb R\backslash \left\{ 1 \right\}\)
Sự biến thiên:
\(\eqalign{
& y’ = {{2{x^2} - 4x} \over {{{(x - 1)}^2}}} \cr
& y’ = 0 \Leftrightarrow \left[ \matrix{
x = 0 \hfill \cr
x = 2 \hfill \cr} \right. \cr} \)
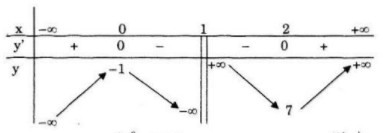
Hàm số đồng biến trên khoảng \(( - \infty ;0)\) và \((2; + \infty )\)
Hàm số nghịch biến trên khoảng \((0;1)\) và \((1;2)\)
Cực trị
Hàm số đạt cực đại tại \(x=0\), \(y_{CĐ}=1\)
Hàm số đạt cực tiểu tại \(x=2\), \(y_{CT}=7\)
Giới hạn:
\(\mathop {\lim y}\limits_{x \to {1^ - }} = - \infty ;\,\mathop {\lim y}\limits_{x \to {1^ + }} = + \infty \)
Tiệm cận đứng là: \(x=1\)
\(\eqalign{
& a = \mathop {\lim }\limits_{x \to \infty } {y \over x} = \mathop {\lim }\limits_{x \to \infty } {{2{x^2} - x + 1} \over {{x^2} - x}} = 2 \cr
& b = \mathop {\lim }\limits_{x \to \infty } (y - 2x) = \mathop {\lim }\limits_{x \to \infty } \left( {{{2{x^2} - x + 1} \over {x - 1}} - 2x} \right) = 1 \cr} \)
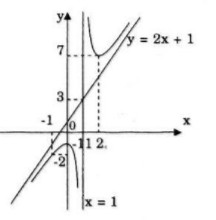
Tiệm cận xiên là: \(y=2x+1\)
Bảng biến thiên:
Advertisements (Quảng cáo)
Đồ thị cắt \(Oy\) tại điểm \((0;-1)\)
b) Hoành độ giao điểm của đường thẳng và đường cong đã cho là nghiệm của phương trình
\(\eqalign{
& {{2{x^2} - x + 1} \over {x - 1}} = m - 1 \Leftrightarrow 2{x^2} - x + 1 = \left( {x - 1} \right)\left( {m - x} \right) \cr
& \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \Leftrightarrow 3{x^2} - \left( {m + 2} \right)x + m + 1 = 0\,\,\left( 1 \right) \cr} \)
(vì \(x =1\) không là nghiệm củ hai phương trình)
Đường thẳng cắt đường cong tại hai điểm phân biệt khi và chỉ khi phương trình (1) có hai nghiệm phân biệt, tức là
\(\eqalign{
& \Delta = {\left( {m + 2} \right)^2} - 12\left( {m + 1} \right) > 0 \Leftrightarrow {m^2} - 8m - 8 > 0 \cr
& \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \Leftrightarrow m < 4 - 2\sqrt 6 \,\,\text{hoặc}\,\,m > 4 + 2\sqrt {6\,\,} \,\,\,\,\left( 2 \right) \cr} \)
c) Hoành độ giao điểm \(A, B\) là các nghiệm của (1)
Hoành độ trung điểm \(M\) của \(AB\) là: \({x_M} = {1 \over 2}\left( {{x_A} + {x_B}} \right) = {{m + 2} \over 6}\)
Vì M nằm trên đường thẳng y = m – x nên \({y_M} = m - {x_M} = m - {{m + 2} \over 6} = {{5m - 2} \over 6}\)
Khử \(m\) từ hệ
\(\left\{ \matrix{
{x_M} = {{m + 2} \over 6} \hfill \cr
{y_M} = {{5m - 2} \over 6} \hfill \cr} \right.\) ta dược: \(5{x_M} - {y_M} = 2 \Leftrightarrow {y_M} = 5{x_M} - 2\)
Vậy \(M\) nằm trên đường thẳng \(y = 5x -2\)
Vì \(m\) chỉ lấy giá trị thỏa mãn (2) nên:
\(m < 4 - 2\sqrt 6 \Rightarrow m = 6{x_M} - 2 < 4 - 2\sqrt 6 \Rightarrow {x_M} < 1 - {{\sqrt 6 } \over 3}\)
\(m > 4 + 2\sqrt 6 \Rightarrow m = 6{x_M} - 2 > 4 + 2\sqrt 6 \Rightarrow {x_M} > 1 + {{\sqrt 6 } \over 3}\)
Vậy tập hợp các trung điểm \(M\) của đoạn \(AB\) là phần của đường thẳng \(y = 5x -2\) với \({x_M} < 1 - {{\sqrt 6 } \over 3}\) hoặc \({x_M} > 1 + {{\sqrt 6 } \over 3}\)
