Bài 1. Xét sự đồng biến, nghịch biến của các hàm số:
a) \(y = 4 + 3x - x^2\) ; b) \(y ={1 \over 3}x^3\) + \(3x^2-7x - 2\) ;
c) \(y = x^4\) - \(2x^2\) +\( 3\) ; d) \(y = -x^3\)+ \(x^2\) - \(5\).

1. a) Tập xác định : \(D =\mathbb R\);
\(y’ = 3 - 2x => y’ = 0 ⇔ x =\) \({3 \over 2}\).
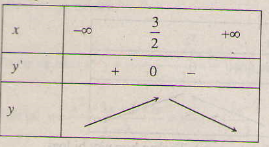
Bảng biến thiên :
 z
z
Hàm số đồng biến trên khoảng \(\left( { - \infty ;{3 \over 2}} \right)\); nghịch biến trên khoảng \(\left( { {3 \over 2}};+\infty \right)\)
b) Tập xác định \(D=\mathbb R\);
\(y’= x^2\)+ \(6x - 7 \Rightarrow y’ = 0 ⇔ x = 1, x = -7\).
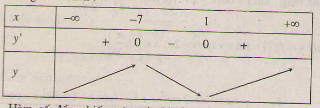
Bảng biến thiên :
Advertisements (Quảng cáo)
Hàm số đồng biến trên các khoảng \((-∞ ; -7), (1 ; +∞)\) ; nghịch biến trên các khoảng \((-7 ; 1)\).
c) Tập xác định : \(D=\mathbb R\).
\(y’ = 4x^3\)-\(4x = 4x(x^2-1)\) \(\Rightarrow y’ = 0 ⇔ x = -1, x = 0, x = 1\).
Bảng biến thiên :
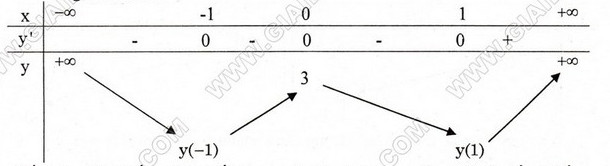
Hàm số đồng biến trên các khoảng \((-1 ; 0), (1 ; +∞)\) ; nghịch biến trên các khoảng \((-∞ ; -1), (0 ; 1)\).
d) Tập xác định :\( D=\mathbb R\).
\(y’ = -3x^2\) +\( 2x \Rightarrow y’ = 0 ⇔ x = 0, x =\) \({2 \over 3}\).
Bảng biến thiên :
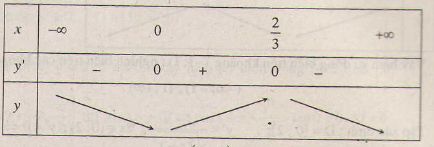
Hàm số đồng biến trên khoảng \(( 0 ; {2 \over 3} )\) ; nghịch biến trên các khoảng \((-∞ ; 0)\), \(({2 \over 3}; +∞)\).
