Bài 10. Giải bài toán sau đây bằng phương pháp tọa độ:
Cho hình lập phương \(ABCD.A’B’C’D’\) có cạnh bằng \(1\). Tính khoảng cách từ đỉnh \(A\) đến các mặt phẳng \((A’BD)\) và \((B’D’C)\).

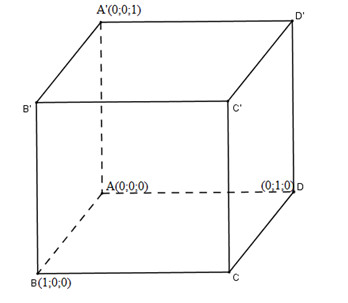
Chọn hệ trục tọa độ \(Oxyz\) sao cho \(A(0 ; 0 ; 0), B(1 ; 0 ; 0), D(0 ; 1; 0), A'(0 ; 0 ; 1)\)
Khi đó
\(B'(1 ; 0 ; 1), D'(0 ; 1 ; 1), C(1 ; 1 ; 0)\). Phương trình mặt phẳng \((A’BD)\) có dạng:
Advertisements (Quảng cáo)
\(x + y + z - 1 = 0\). (1)
\(\overrightarrow{CB’}(0 ; -1 ; 1)\) ; \(\overrightarrow{CD’}(-1 ; 0 ; 1)\).
Mặt phẳng \((B’D’C)\) qua điểm \(C\) và nhận \(\overrightarrow{n}=\left [\overrightarrow{CB’},\overrightarrow{CD’} \right ] = (-1 ; -1 ; -1 )\) làm vectơ pháp tuyến. Phương trình mặt phẳng \((B’D’C)\) có dạng:
\(x + y + z - 2 = 0\) (2)
Ta có \(d_{1}(A,(A’BD))=\frac{1}{\sqrt{3}}.\)
\(d_{2}(A,(B’D’C))=\frac{2}{\sqrt{3}}.\)
