
Cho hai góc kề bù \(\widehat {AOB}\) và \(\widehat {BOC}\), biết rằng \(\widehat {AOB} = 2\widehat {BOC}\). Vẽ tia OM là phân giác của góc BOC. Hãy tính số đo của góc AOM.

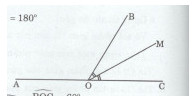
Hai góc AOB và BOC kề bù nên: \(\widehat {AOB} + \widehat {BOC} = {180^0}.\)
Mà \(\widehat {AOB} = 2\widehat {BOC} \Rightarrow 2\widehat {BOC} + \widehat {BOC} = {180^0}.\)
\( \Rightarrow 3\widehat {BOC} = {180^0} \Rightarrow \widehat {BOC} = {{{{180}^0}} \over 3} = {60^0}.\)
Advertisements (Quảng cáo)
Vậy \(\widehat {AOB} = {2.60^0} = {120^0}.\)
OM là tia phân giác của góc \(\widehat {BOC} \Rightarrow \widehat {BOM} = \widehat {COM} = {{\widehat {BOC}} \over 2} = {{{{60}^0}} \over 2} = {30^0}.\)
Vì góc AOC là góc bẹt nên tia OM nằm giữa hai tia OC và OA.
Do đó: \(\widehat {COM} + \widehat {AOM} = {180^0}\)
\(\Rightarrow \widehat {AOM} = {180^0} - \widehat {COM} = {180^0} - {30^0} = {150^0}.\)
