
Cho hai góc kề bù \(\widehat {AOB}\) và \(\widehat {AOC}\), biết rằng \(\widehat {AOB} = {120^o}\).
a) Tính số đo góc AOC.
b) Gọi OE là tia phân giác của goác AOB. Hãy tính số đo góc EOC.
c) Tia OA có phải là tia phân giác của góc EOC không ? Vì sao ?

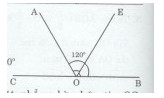
a)Vì hai góc AOB và AOC kề bù nên \(\widehat {AOB} + \widehat {AOC} = {180^0}.\)
Advertisements (Quảng cáo)
Do đó: \(\widehat {AOC} = {180^0} - \widehat {AOB} = {180^0} - {120^0} = {60^0}.\)
b) OE là tia phân giác của góc AOB.
Nên: \(\widehat {EOB} = \widehat {EOA} = {{\widehat {AOB}} \over 2} = {{{{120}^0}} \over 2} = {60^0}.\)
Vì hai góc COE và EOB kề bù nên \(\widehat {COE} + \widehat {EOB} = {180^0}.\)
Do đó: \(\widehat {COE} = {180^0} - \widehat {EOB} = {180^0} - {60^0} = {120^0}.\)
c) Hai tia OA, OE cùng nằm trên một nửa mặt phẳng bờ chứa tia OC, \(\widehat {COA} < \widehat {COE}({60^0} < {120^0})\) nên tia OA nằm giữa hai tia OC và OE.
Mặt khác: \(\widehat {COA} = \widehat {AOE} = {{\widehat {COE}} \over 2}( = {60^0}) \Rightarrow \) Tia OA là tia phân giác của góc COE.
