Quan sát Hình 29, biết a // b, \(3\widehat {{A_1}} = 2\widehat {{A_2}}\). Tìm số đo mỗi góc của đỉnh A và B.
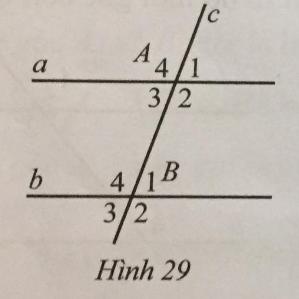
Tính số đo mỗi góc của hai đỉnh dựa vào tính chất của hai đường thẳng song song: các góc đồng vị, so le trong (ngoài) bằng nhau; trong cùng phía bù nhau bằng nhau.
Ta có \(3\widehat {{A_1}} = 2\widehat {{A_2}}\) hay \(\widehat {{A_2}} = \dfrac{3}{2}\widehat {{A_1}}\) và \(\widehat {{A_1}} + \widehat {{A_2}} = 180^\circ \) (hai góc kề bù) nên
\(\begin{array}{l}\widehat {{A_1}} + \dfrac{3}{2}\widehat {{A_1}} = \dfrac{5}{2}\widehat {{A_1}} = 180^\circ \to \widehat {{A_1}} = 72^\circ \\ \Rightarrow \widehat {{A_2}} = \dfrac{3}{2}{\rm{ }}{\rm{. }}72^\circ = 108^\circ \end{array}\)
Mà a // b nên \(\widehat {{A_3}} = \widehat {{B_1}} = \widehat {{A_1}} = \widehat {{B_3}} = 72^\circ \) , \(\widehat {{A_4}} = \widehat {{B_2}} = \widehat {{A_2}} = \widehat {{B_4}} = 108^\circ \) (các góc so le trong và đồng vị).