Cho tam giác ABC cân tại A có AB = AC = 10cm, BC = 12cm. Vẽ cung tròn tâm A có bán kính 9cm. Cung đó có cắt đường thẳng BC hay không có cắt cạnh BC hay không? Vì sao?

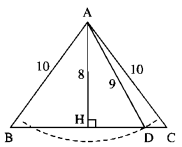
\(AH \bot BC\)
\(\widehat {AHB} = \widehat {AHC} = 90^\circ \)
Advertisements (Quảng cáo)
\(HB = HC = {{BC} \over 2} = 6\left( {cm} \right)\)
\(\widehat {AHB} = 90^\circ \)
\(\eqalign{
& A{B^2} = A{H^2} + H{B^2} \cr
& A{H^2} = A{B^2} - H{B^2} \cr
& A{H^2} = {10^2} - {6^2} = 64 \cr
& AH > 0 \Rightarrow AH = 8\left( {cm} \right) \cr} \)
Do bán kính cung tròn 9 (cm) > 8 (cm) nên cung tròn tâm A bán kính 9 cm cắt đường thẳng BC. Gọi D là giao điểm của cung tròn tâm A bán kính 9 cm. Với BC ta có đường xiên AD > AC nên hình chiếu HD < HC do đó D nằm giữa H và C. Vậy cung tròn tâm A bán kính 9cm cắt cạnh BC.
