Cho tam giác ABC có AB < AC. Tia phân giác của góc A cắt BC ở D. So sánh các độ dài BD, DC.

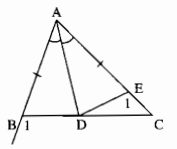
Trên cạnh AC lấy điểm E sao cho AE = AB
AB < AC nên AE < AC => E nằm giữa A và C
Xét ∆ABD và ∆AED:
AB = AE (theo cách vẽ)
\(\widehat {BA{\rm{D}}} = \widehat {E{\rm{AD}}}\left( {gt} \right)\)
AD cạnh chung
Do đó: ∆ABD = ∆AED (c.g.c)
=> BD = DE (2 cạnh tương ứng)
Advertisements (Quảng cáo)
\( \Rightarrow \widehat {AB{\rm{D}}} = \widehat {A{\rm{ED}}}\) (2 góc tương ứng)
\(\widehat {AB{\rm{D}}} + \widehat {{B_1}} = 180^\circ \) (2 góc kề bù)
\(\widehat {A{\rm{ED}}} + \widehat {{E_1}} = 180^\circ \) (2 góc kề bù)
Suy ra: \(\widehat {{B_1}} = \widehat {{E_1}}\)
Trong ∆ABC ta có \(\widehat {{B_1}}\) là góc ngoài tại đỉnh B.
\( \Rightarrow \widehat {{B_1}} > \widehat C\) (tính chất góc ngoài tam giác)
Suy ra: \(\widehat {{E_1}} > \widehat C\)
Trong ∆DEC ta có: \(\widehat {{E_1}} > \widehat C\)
\( \Rightarrow \) DC > DE (đối diện góc lớn hơn là cạnh lớn hơn)
Suy ra: BD < DC.
