Chứng minh rằng AB < AD < AC.. Câu 3 trang 36 Sách Bài Tập (SBT) Toán lớp 7 tập 2 - Bài 1: Quan hệ giữa góc và cạnh đối diện trong một tam giác
Cho tam giác ABC có \(\widehat B > 90^\circ \), điểm D nằm giữa B và C. Chứng minh rằng AB < AD < AC

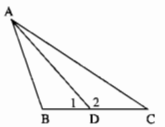
Trong ∆ABC ta có: \(\widehat B > 90^\circ \)
\( \Rightarrow \widehat B > {\widehat D_1}\)
Advertisements (Quảng cáo)
Nên AD > AB (đối diện góc lớn hơn là cạnh lớn hơn) (1)
Trong ∆ABD ta có \(\widehat {{D_2}}\) là góc ngoài tại đỉnh nên \(\widehat {{D_2}} > \widehat B > 90^\circ \)
Trong ∆ADC ta có: \(\widehat {{D_2}} > 90^\circ \Rightarrow \widehat {{D_2}} > \widehat C\)
Nên AC > AD (đối diện góc lớn hơn là cạnh lớn hơn) (2)
Từ (1) và (2) suy ra: AB < AD < AC.
