Câu 1.4 trang 37 Sách Bài Tập (SBT) Toán lớp 7 tập 2
Cho tam giác ABC với AB ≥ AC. Trên cạnh BC lấy một điểm M bất kỳ khác B và C. Chứng minh rằng AM < AC.
Giải
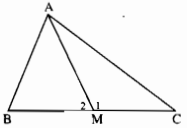
Ta có \(\widehat {{M_1}} + \widehat {{M_2}} = 180^\circ \) nên chỉ có hai khả năng xảy ra ứng với các vị trí của M trên BC là \(\widehat {{M_1}} > 90^\circ \) hoặc \(\widehat {{M_2}} \ge 90^\circ \).
- Nếu \(\widehat {{M_1}} > 90^\circ \) thì tam giác AMC có góc tù nên AM > AC
- Nếu \(\widehat {{M_2}} \ge 90^\circ \) thì trong tam giác ABM có AM < AB. Kết hợp với giả thiết AB < AC, ta suy ra AM < AC. Vậy ta luôn có AM < AC.
Câu 1.5 trang 38 Sách Bài Tập (SBT) Toán lớp 7 tập 2
Cho tam giác ABC với AB ≤ BC ≤ CA. Trên các cạnh BC và AC lần lượt lấy hai điểm M và N (khác A, B, C). Chứng minh rằng MN < AC.
Giải
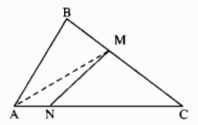
Kẻ đoạn thẳng AM. Xét tam giác MAC. Chứng minh tương tự như bài 1.4 ta có MN < a, trong đó a là đoạn lớn nhất trong hai đoạn thẳng MA và MC. Nếu ta chứng minh được
Advertisements (Quảng cáo)
MA < AC và MC < AC thì sẽ suy ra được a < AC, từ đó có MN < AC.
Trong tam giác ABC có AB ≤ AC, M ∈ BC (M # B, M # C); Chứng minh tương tự bài 1.4, ta có AM < AC. Mặt khác MC < BC ≤ CA. Vậy a < AC, suy ra MN < AC.
Câu 1.6 trang 38 Sách Bài Tập (SBT) Toán lớp 7 tập 2
Cho tam giác ABC có góc A tù. Trên cạnh AB lấy điểm D (khác A và B), trên cạnh AC lấy điểm E (khác A và C). Chứng minh rằng DE < BC.
Giải
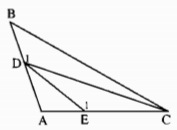
Xét tam giác CDE. Ta có \(\widehat E > \widehat A\), mà Â là góc tù nên \(\widehat {{E_1}}\) là góc tù.
Suy ra CD > DE (1)
Xét tam giác BCD. Ta có \(\widehat {{D_1}} > \widehat A\) nên \(\widehat {{D_1}}\) là góc tù.
Suy ra BC > CD (2)
Từ (1) và (2) suy ra BC > DE.
