Cho tam giác ABC. Trên cạnh AB lấy các điểm D và E sao cho AD = BE. Qua D và E, vẽ các đường thẳng song song với BC, chúng cắt AC theo thứ tự ở M và N. Chứng minh rằng DM + EN = BC.
Hướng dẫn: Qua N, kẻ đường thẳng song song với AB.

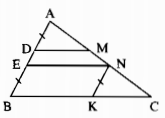
Từ N kẻ đường thẳng song song với AB cắt BC tại K. Nối EK.
Xét ∆BEK và ∆NKE, ta có:
\(\widehat {EKB} = \widehat {KEN}\) (so le trong vì EN // BC)
EK cạnh chung
\(\widehat {BEK} = \widehat {NKE}\) (so le trong vì NK // AB)
Suy ra: ∆BEK = ∆NKE (g.c.g)
Advertisements (Quảng cáo)
Suy ra: BE = NK (hai cạnh tương ứng)
EN = BK (hai cạnh tương ứng)
Xét ∆ADM và ∆NKC, ta có:
\(\widehat A = \widehat {KNC}\) (đồng vị vì NK // AB)
AD = NK (vì cùng bằng BE)
\(\widehat {A{\rm{D}}M} = \widehat {NKC}\) (vì cùng bằng \(\widehat B\))
Suy ra: ∆ADM = ∆NKC (c.g.c)
=>DM = KC (hai cạnh tương ứng)
Mà BC = BK + KC. Suy ra: BC = EN + DM
