Cho tam giác ABC, D là trung điểm của AB, E là trung điểm của AC. Vẽ điểm F sao cho E là trung điểm của DF. Chứng minh rằng:
a) DB = CF
b) ∆BDC = ∆FCD
c) DE// BC và \(DE = {1 \over 2}BC\)

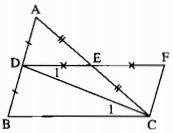
a) Xét ∆ADE và ∆CFE, ta có:
AE = CE (gt)
\(\widehat {A{\rm{ED}}} = \widehat {{\rm{CEF}}}\) (đối đỉnh)
DE = FE(gt)
Suy ra: ∆ADE = ∆CFE (c.g.c)
\( \Rightarrow \) AD = CF (hai cạnh tương ứng)
Mà AD = DB (gt)
Vậy: DB = CF
b) Ta có: ∆ADE = ∆CFE (chứng minh trên)
Advertisements (Quảng cáo)
\( \Rightarrow \widehat {A{\rm{D}}E} = \widehat {CF{\rm{E}}}\) (2 góc tương ứng)
\( \Rightarrow \) AD // CF (vì có cặp góc so le trong bằng nhau)
Hay AB // CF
Xét ∆DBC = ∆CDF, ta có:
BD = CF (chứng minh trên)
\(\widehat {B{\rm{D}}C} = \widehat {FC{\rm{D}}}\) (hai góc so le trong vì CF // AB)
DC cạnh chung
Suy ra: ∆BDC = ∆FCD(c. g. c)
c) Ta có: ∆BDC = ∆FCD (chứng minh trên)
Suy ra: \(\widehat {{C_1}} = \widehat {{D_1}}\) (hai góc tương ứng)
Suy ra: DE // BC (vì có hai góc so le trong bằng nhau)
BDC = ∆FCD=> BC = DF (hai cạnh tương ứng)
Mà \({\rm{D}}E = {1 \over 2}DF\left( {gt} \right)\). Vậy \({\rm{D}}E = {1 \over 2}BC\)
