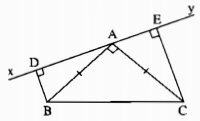
Cho tam giác ABC vuông tại A có AB = AC. Qua A kẻ đường thẳng xy (B, C nằm cùng phía đối với xy). Kẻ BD và CE vuông góc với xy. Chứng minh rằng:
a) ∆BAD = ∆ACE
b) DE = BD + CE

a) Ta có: \(\widehat {BA{\rm{D}}} + \widehat {BAC} + \widehat {CA{\rm{E}}} = 180^\circ \) (kề bù)
Mà \(\widehat {BAC} = 90^\circ \left( {gt} \right) \Rightarrow \widehat {BA{\rm{D}}} + \widehat {CA{\rm{E}}} = 90^\circ \) (1)
Trong ∆AEC, ta có:
\(\widehat {A{\rm{E}}C} = 90^\circ \Rightarrow \widehat {CA{\rm{E}}} + \widehat {AC{\rm{E}}}{\rm{ = 90}}^\circ \) (2)
Từ (1) và (2) suy ra: \(\widehat {BA{\rm{D}}} = \widehat {AC{\rm{E}}}\)
Advertisements (Quảng cáo)
Xét hai tam giác vuông AEC và BDA, ta có:
\(\widehat {A{\rm{E}}C} = \widehat {B{\rm{D}}A} = 90^\circ \)
AC = AB (gt)
\(\widehat {AC{\rm{E}}} = \widehat {BA{\rm{D}}}\) (chứng minh trên)
Suy ra: ∆AEC = ∆BDA (cạnh huyền, góc nhọn)
b) Ta có: ∆AEC = ∆BDA
=> AE = BD và EC = DA
Mà DE = DA + AE
Vậy: DE = CE + BD
