Chứng minh rằng AD là tia phân giác của góc A.. Câu 93 trang 151 Sách Bài Tập (SBT) Toán lớp 7 tập 1 - Bài 8: Các trường hợp bằng nhau của tam giác vuông
Cho tam giác ABC cân tại A. Kẻ AD vuông góc với BC. Chứng minh rằng AD là tia phân giác của góc A.

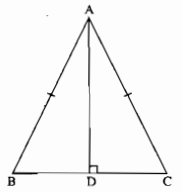
Xét tam giác vuông ADB và ADC, ta có:
\(\widehat {A{\rm{D}}B} = \widehat {A{\rm{D}}C} = 90^\circ \)
AB = AC (gt)
Advertisements (Quảng cáo)
AD cạnh chung
Suy ra:
∆ADB = ∆ADC (cạnh huyền, cạnh góc vuông)
\( \Rightarrow \widehat {BA{\rm{D}}} = \widehat {CA{\rm{D}}}\) (hai góc tương ứng)
Vậy AD là tia phân giác \(\Rightarrow \widehat {BA{\rm{D}}} = \widehat {CA{\rm{D}}}\)
