
Cho tam giác ABC cân tại A, đường cao AD, G là trọng tâm. Trên tia đối của tia DG lấy điểm E sao cho DE = DG.
a) Chứng minh rằng BG = GC = CE = BE.
b) Chứng minh \(\Delta ABE = \Delta ACE\)
c) Nếu \(CG = {1 \over 2}AE\) thì tam giác ABC là tam giác gì ? Vì sao ?

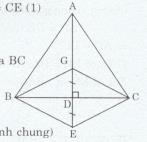
a) Ta có:\(BC \bot GE\) tại D (gt) và D là trung điểm của GE (DE =DG, \(D \in EG\))
=> BC là đường trung trực của GE
=> BG = BE và GC = CE (1)
∆ABC cân tại A có AD là đường cao (gt)
=> AD là đường trung tuyến => D là trung điểm của BC
Mà \(GE \bot BC\) tại D (gt). Nên GE là đường trung trực của BC
=> BG = GC và BE = CE (2)
Advertisements (Quảng cáo)
Từ (1) và (2) suy ra BG = GC = CE = BE.
b) Xét ∆ABE và ∆ACE ta có:
AB = AC (∆ABC cân tại A), BE = EC (câu a) và AE (cạnh chung)
Do đó: ∆ABE = ∆ACE (c.c.c).
c) ∆ABC cân tại A có AD là đường cao (gt)
=> AD là đường phân giác của góc BAC \( \Rightarrow \widehat {BAC} = 2\widehat {GAC}\)
∆ABC có G là trọng tâm, AD là đường trung tuyến \( \Rightarrow AG = {2 \over 3}AD\)
Do đó \(DE = DG = {1 \over 3}AD.\) Nên \(AG = EG = {1 \over 2}AE\)
Mà \(CG = {1 \over 2}AE\) (gt). Nên EG = GC = AG
Mà CE = GC. Ta có EG = GC = CE => ∆GEC đều \( \Rightarrow \widehat {EGC} = 60^\circ\)
Mà AG = GC (= GE) => ∆GAC cân tại G \( \Rightarrow \widehat {GAC} = \widehat {GCA}\)
Do đó \(\widehat {GAC} = {1 \over 2}\widehat {EGC} = {1 \over 2}.60^\circ = 30^\circ\). Nên \(\widehat {BAC} = 2\widehat {GAC} = 60^\circ\)
∆ABC cân tại A có \(\widehat {BAC} = 60^\circ\). Do đó ∆ABC đều.
