
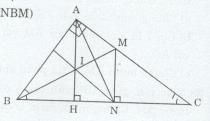
Cho tam giác ABC vuông tại A (AB < AC). Tia phân giác của góc B cắt AC tại M. Kẻ MN vuông góc với BC \(\left( {N \in BC} \right)\)
a) Chứng minh rằng tam giác ABM bằng tam giác NBM.
b) Chứng minh AN vuông góc với BM.
c) Kẻ đường cao AH của tam giác ABC. Chứng minh AN là tia phân giác của góc HAM.
d) Gọi I là giao điểm của AH với BM. Chứng minh rằng NI vuông góc với ABN.

a) Xét ∆ABM \((\widehat A = 90^\circ )\) và ∆NBM \((\widehat N = 90^\circ )\)
Ta có: BM (cạnh chung)
\(\widehat {ABM} = \widehat {NBM}\) (BM là tia phân giác của \(\widehat {ABC}\))
Do đó: ∆ABM = ∆NBM (cạnh huyền – góc nhọn).
b) Ta có BA = BN và MA = MN (∆ABM = ∆NBM)
Advertisements (Quảng cáo)
=> BM là đường trung trực của AN
\( \Rightarrow BM \bot AN.\)
c) Ta có AM = NM (∆ABM = ∆NBM)
=> ∆AMN cân tại M
\( \Rightarrow \widehat {MNA} = \widehat {NAM}\)
Mà \(\widehat {MNA} = \widehat {NAH}\) (hai góc so le trong và AH // MN (vì cùng vuông góc với BC))
Nên \(\widehat {NAM} = \widehat {NAH} \Rightarrow\) AH là tia phân giác của \(\widehat {HAM}.\)
d) BA = BN (∆ABM = ∆NBM) => ∆ABN cân tại B.
Mà BI là đường phân giác của ∆ABN (gt). Nên BI cũng là đường cao của ∆ABN.
Lại có AH là đường cao của ∆ABN (\(AH \bot BN\) tại H) và BI cắt AH tại I (gt)
=> I là trực tâm của ∆ABN => NI là đường cao của ∆ABN \( \Rightarrow NI \bot AB.\)
