
Cho tam giác ABC cân tại A có góc A nhọn. Tia phân giác của góc BAC cắt BC tại M.
a) Chứng minh rằng \(\Delta AMB = \Delta AMC\)
b) Vẽ trung tuyến CE của tam giác ABC cắt AM tại G. Chứng minh G là trọng tâm của tam giác ABC.
c) Biết độ dài BM = 12 cm, AB = 20 cm. Tính độ dài AG.
d) Qua M kẻ đường thẳng song song với AB cắt AC tại N. Chứng minh ba điểm A, G, N thẳng hàng.

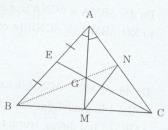
a) Xét ∆AMB và ∆AMC ta có:
AM (cạnh chung)
\(\widehat {BAM} = \widehat {MAC}\) (AM là tia phân giác của \(\widehat {BAC}\))
Và AB = AC (∆ABC cân tại A)
Do đó: ∆AMB = ∆AMC (c.g.c).
b) ∆ABC cân tại A có AM là đường phân giác (gt)
=> AM là đường trung tuyến của ∆ABC.
Mà CE là đường trung tuyến của ∆ABC (gt) và AM cắt CE tại G (gt)
Nên G là trọng tâm của ∆ABC.
Advertisements (Quảng cáo)
c) ∆ABC cân tại A có AM là đường phân giác (gt)
=> AM là đường cao của ∆ABC \( \Rightarrow AM \bot BC\) tại M => ∆ABM vuông tại M
=> AM2 + BM2 = AB2 (định lí Pythagore)
=> AM2 + 122 = 202 => AM2 = 256 = 162 => AM = 16 (cm)
∆ABC có AM là đường trung tuyến (câu b) và G là trọng tâm (câu b)
\( \Rightarrow AG = {2 \over 3}AM = {2 \over 3}.16 = {{32} \over 3}(cm).\)
d) Ta có: \(\widehat {ABC} = \widehat {NCM}\) (∆ABC cân tại A)
\(\widehat {ABC} = \widehat {NMC}\) (hai góc đồng vị và MN // AB)
Do đó \(\widehat {NCM} = \widehat {NMC}\) => ∆NCM cân tại N => NM = NC (1)
Mặt khác: \(\widehat {BAM} = \widehat {AMN}\) (hai góc so le trong và AB // MN)
\(\widehat {BAM} = \widehat {MAN}\) (AM là tia phân giác của \(\widehat {BAC}\))
\( \Rightarrow \widehat {AMN} = \widehat {MAN}\) => ∆AMN cân tại N => NM = NA (2)
Từ (1) và (2) suy ra NC = NA
=> N là trung điểm của AC (\(N \in AC\)) => BN là đường trung tuyến của ∆ABC
Mà G là trọng tâm của ∆ABC (câu b). Nên BN đi qua G
Vậy B, G, N thẳng hàng.
