Luyện tập - Chủ đề 6 : Các đường đồng quy của tam giác - Bài tập 32 trang 124 Tài liệu dạy – học Toán 7 tập 2. Giải bài tập Cho tam giác MNP cân tại M (MN = MP > NP). Đường trung trực của MP tại D cắt đường thẳng NP tại E. Trên tia đối của tia DE lấy điểm F sao cho MF = EP.

Cho tam giác MNP cân tại M (MN = MP > NP). Đường trung trực của MP tại D cắt đường thẳng NP tại E. Trên tia đối của tia DE lấy điểm F sao cho MF = EP.
a) Chứng minh rằng góc EMP bằng góc EPM.
b) Chứng minh tam giác EPF cân.

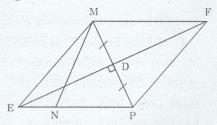
a) Ta có E thuộc đường trung trực của MP (gt)
=> EM = EP
Advertisements (Quảng cáo)
=> ∆EMP cân tại E
\( \Rightarrow \widehat {EMP} = \widehat {EPM}.\)
b) F thuộc đường trung trực của MP
=> MF = FP và MF = EP (gt)
=> EP = FP
Vậy ∆PEF cân tại P.
