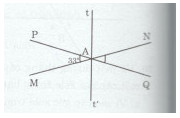
Cho hai đường thẳng MN và PQ cắt nhau tạo thành \(\widehat {PAM} = {33^o}\) (h.15).
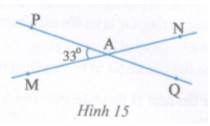
a) Tính số đo các góc còn lại.
b) Vẽ At là tia phân giác cỉa góc PAN. Hãy tính số đo góc của góc tAQ và góc MAQ. Vẽ tia At’ là tia đối của tia At. Chứng tỏ rằng At’ là tia phân giác của góc MAQ.

a)Hai góc NAQ và PAM là hai góc đối đỉnh nên \(\widehat {NAQ} = \widehat {PAM} = {33^0}\)
Hai góc MAP và PAN là hai góc kề bù \( \Rightarrow \widehat {MAP} + \widehat {PAN} = {180^0}\)
Do đó: \(\widehat {PAN} = {180^0} - {33^0} = {147^0}\)
Advertisements (Quảng cáo)
Hai góc \(\widehat {PAN}\) và \(\widehat {MAQ}\) là 2 góc đối đỉnh nên \(\widehat {MAQ} = \widehat {PAN} = {147^0}\)
b) At là tia phân giác của \(\widehat {PAN}\) nên \(\widehat {PAt} = \widehat {tAN}\)
At’ là tia đối của tia At nên hai góc Pat và Qat’ là hai góc đối đỉnh; góc Nat và Mat’ là hai góc đối đỉnh.
Ta có: \(\widehat {MAt’} = \widehat {NAt}\) (hai góc đối đỉnh).
Và \(\widehat {QAt’} = \widehat {PAt}\) (hai góc đối đỉnh)
Do đó: \(\widehat {MAt’} = \widehat {QAt’}\)
Vậy At’ là tia phân giác của góc MAQ.