
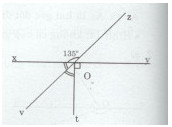
Cho đường thẳng xy đi qua điểm O. Vẽ tia Oz sao cho \(\widehat {xOz} = {135^o}\) . Trên nửa mặt phẳng bờ xy không chứa tia oz vẽ tia Ot sao cho \(\widehat {yOt} = {90^o}\). Gọi Ov là tia phân giác của \(\widehat {xOt}\).
a) Chứng tỏ rằng Oz và Ov là hai tia đối nhau.
b) Các góc \(\widehat {xOv}\) và \(\widehat {yOz}\) có phải là hai góc đối đỉnh không ? Vì sao ?

a)Ta có góc xOz và zOy là hai góc kề bù.
Nên \(\widehat {xOz} + \widehat {zOy} = {180^0} \Rightarrow \widehat {zOy} = {180^0} - {135^0} = {45^0}\)
Advertisements (Quảng cáo)
Ta có: \(\widehat {xOv} = \widehat {vOt} = {{\widehat {xOt}} \over 2} = {{{{90}^0}} \over 2} = {45^0}\)
(Do Ov là tia phân giác góc xOt)
Ta có: \(\widehat {v0x} + \widehat {xOz} = {45^0} + {135^0} = {180^0}.\)
Do đó Oz và Ov là hai tia đối nhau.
b)*\(\widehat {xOv} = \widehat {yOz}( = {45^0})\) nên \(\widehat {xOv}\) và \(\widehat {yOz}\) là hai góc đối đỉnh.
