
Cho hai đường thẳng MN và PQ cắt nhau tạo hành bốn góc, trong đó tổng ba trong bốn góc có số đo là 290o (h.16). Tính số đo của các góc đó.
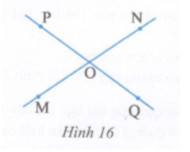

Theo hình vẽ ta có: \(\widehat {PON} + \widehat {NOQ} + \widehat {MOQ} = {290^0}\)
Mà \(\widehat {PON} + \widehat {NOQ} = {180^0}\) (hai góc kề bù). Nên \(\widehat {MOQ} = {290^0} - {180^0} = {110^0}\)
Advertisements (Quảng cáo)
Ta có: \(\widehat {PON}\) và \(\widehat {MOQ}\) là hai góc đối đỉnh. \( \Rightarrow \widehat {PON} = \widehat {MOQ} = {110^0}\)
\(\widehat {PON}\) và \(\widehat {NOQ}\) là hai góc kề bù.
\( \Rightarrow \widehat {PON} + \widehat {NOQ} = {180^0} \Rightarrow \widehat {NOQ} = {180^0} - {110^0} = {70^0}\)
\(\widehat {POM}\) và \(\widehat {NOQ}\) là hai góc đối đỉnh \( \Rightarrow \widehat {POM} = \widehat {NOQ} = {70^0}\)
