
Cho tam giác DEF vuông tại D, phân giác của góc E cắt DF tại A. Trên EF lấy điểm B sao cho EB = ED.
a) Chứng minh rằng \(\Delta DEA = \Delta BEA\)
b) Chứng minh rằng \(AB \bot EF\)

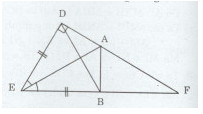
a)Xét tam giác DEA và BEA có:
ED = EB (gt)
\(\widehat {DEA} = \widehat {BEA}\) (EA là tia phân giác của góc DEB)
Advertisements (Quảng cáo)
EA là cạnh chung.
Do đó: \(\Delta DEA = \Delta BEA(c.g.c)\)
b) Ta có: \(\Delta DEA = \Delta BEA \Rightarrow \widehat {DAE} = \widehat {BAE}\)
Tam giác ADE vuông tại D có: \(\widehat {DEA} + \widehat {DAE} = {90^0}\)
Mà \(\widehat {DEA} = \widehat {AEB}\) (EA là tia phân giác của góc DEB) và \(\widehat {DAE} = \widehat {BAE}\)
Nên \(\widehat {DEA} + \widehat {DAE} = {90^0} \Leftrightarrow \widehat {AEB} + \widehat {BAE} = {90^0}.\)
Mặt khác: \(\widehat {ABF} = \widehat {AEB} + \widehat {BAE}\) (góc ngoài của tam giác ABE)
Do đó: \(\widehat {ABF} = {90^0} \Rightarrow AB \bot EF\)
