Bài tập - Chủ đề 1: Góc tạo bởi các đường thẳng - Bài tập 8 trang 116 Tài liệu dạy – học Toán 7 tập 1. Giải bài tập Cho hai đường thẳng xx’ và yy’ cắt nhau tại O. Gọi Ot là tia phân giác của góc xOy; vẽ tia Ot’ là tia phân giác của góc x’Oy’. Hãy chứng tỏ rằng Ot’ là tia đối của tia Ot.
Cho hai đường thẳng xx’ và yy’ cắt nhau tại O. Gọi Ot là tia phân giác của góc xOy; vẽ tia Ot’ là tia phân giác của góc x’Oy’. Hãy chứng tỏ rằng Ot’ là tia đối của tia Ot.
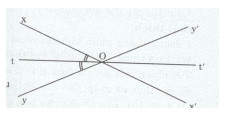
Ta có: \(\widehat {xOy} = \widehat {x’Oy’}\) (hai góc đối đỉnh).
\(\widehat {xOt} = {1 \over 2}\widehat {xOy}\) (Ot là tia phân giác của góc xOy)
Advertisements (Quảng cáo)
\(\widehat {x’Ot’} = {1 \over 2}\widehat {x’Oy’}\) (Ot’ là tia phân giác của góc x’Oy’).
Do đó: \(\widehat {xOt} = \widehat {x’Ot’}\)
Mà \(\widehat {xOt’} + \widehat {x’Ot’} = {180^0}\) (hai góc kề bù)
Nên \(\widehat {xOt’} + \widehat {xOt} = {180^0}\)
Suy ra hai tia Ot và Ot’ là hai tia đối nhau.