Bài 1. Tính số đo \(x\) và \(y\) ở các hình 47.48.49,50,51:
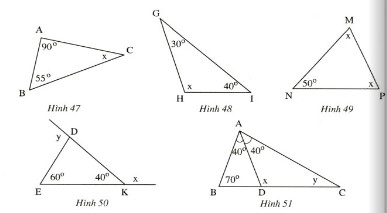

Hình 47)
Theo dịnh lí tổng ba góc trong một tam giác ta được:
\(x + {{90}^0} + {{55}^{0}} = {{180}^0}\)
\(\Rightarrow x = {{180}^0} - \left( {{{90}^0} + {{55}^0}} \right) = {{35}^0}\)
Hình 48)
Theo dịnh lí tổng ba góc trong một tam giác ta được:
\(x + {\rm{ }}{{40}^0} + {\rm{ }}{{30}^0} = {\rm{ }}{{180}^0}\)
\(= > {\rm{ }}x = {\rm{ }}{{180}^0}{\rm{ - }}\left( {{\rm{ }}{{40}^0} + {\rm{ }}{{30}^0}} \right) = {\rm{ }}{{110}^0}\)
Hình 49)
Theo dịnh lí tổng ba góc trong một tam giác ta được:
\(x + {\rm{ }}x + {\rm{ }}{{50}^0} = 180^0\)
\( \Rightarrow {\rm{ }}2x = {\rm{ }}{{180}^0} - {{50}^0} = {{130}^0}\)
\(x = {65}^0\)
Hình50)
Vì \(y\) là góc ngoài tam giác nên ta có:
Advertisements (Quảng cáo)
\(y = {\rm{ }}{60^0} + {\rm{ }}{40^0} = {\rm{ }}{100^0}\)
Hai góc \(x\) và \(\widehat{DKE}\) là hai góc kề bù nên:
\(x + {{40}^0} ={180}^{0}\)
\(x = {{180}^0} - {{40}^{0}} = 140^0\)
Hình 51)
Áp dụng định lí tổng ba góc trong một tam giác vào \(\Delta ABC\) ta có:
\(\widehat A + \widehat B + \widehat C\)
\(({40^0} + {\rm{ }}{40^0}){\rm{ }} + {\rm{ }}{70^0} + {\rm{ }}y{\rm{ }} = {180^0}\)
\(y+ 150^0 =180^0\)
\(y = {180^{0}} - {\rm{ }}{150^0} = {\rm{ }}{30^{0}}\)
Áp dụng định lí tổng ba góc trong một tam giác vào \(\Delta ACD\) ta có:
\(x + {\rm{ }}{40^0} + {\rm{ }}{30^0} = {\rm{ }}{180^0}\)
\(x = {\rm{ }}{180^0} - ({\rm{ }}{40^0} + {\rm{ 3}}{0^0}) = {\rm{ }}{110^0}\)
