Bài 34. Trên mỗi hình 98,99 có tam giác nào bằng nhau? Vì sao?. Bài 34 trang 123 - Sách giáo khoa toán 7 tập 1 - Trường hợp bằng nhau thứ ba của tam giác góc - cạnh - góc (G.C.G)
Bài 34. Trên mỗi hình 98,99 có tam giác nào bằng nhau? Vì sao?
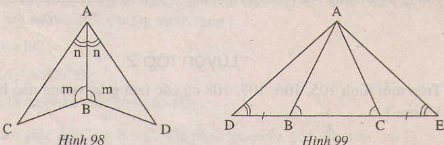
Xem hình 98)
∆ABC và ∆ABD có:
\(\widehat{A_{1}}\)=\(\widehat{A_{2}}\)(gt)
AB là cạnh chung.
\(\widehat{B_{1}}\)=\(\widehat{B_{2}}\)(gt)
Nên ∆ABC=∆ABD(g.c.g)
Xem hình 99)
Ta có:
\(\widehat{B_{1}}\)+\(\widehat{B_{2}}\)=1800 (Hai góc kề bù).
\(\widehat{C _{1}}\)+ \(\widehat{C _{2}}\)=1800 (Hai góc kề bù)
Advertisements (Quảng cáo)
Mà \(\widehat{B_{2}}\)=\(\widehat{C _{2}}\)(gt)
Nên \(\widehat{B_{1}}\)=\(\widehat{C _{1}}\)
* ∆ABD và ∆ACE có:
\(\widehat{B_{1}}\)=\(\widehat{C _{1}}\)(cmt)
BD=EC(gt)
\(\widehat{D }\) = \(\widehat{E }\)(gt)
Nên ∆ABD=∆ACE(g.c.g)
* ∆ADC và ∆AEB có:
\(\widehat{D }\)=\(\widehat{E }\)(gt)
\(\widehat{C _{2}}\)=\(\widehat{B_{2}}\)(gt)
DC=EB
Nên ∆ADC=∆AEB(g.c.g)