Bài 37. Trên mỗi hình 101,102,103 có tam giác nào bằng nhau? Vì sao?. Bài 37 trang 123 - Sách giáo khoa toán 7 tập 1 - Trường hợp bằng nhau thứ ba của tam giác góc - cạnh - góc (G.C.G)
Bài 37. Trên mỗi hình 101,102,103 có tam giác nào bằng nhau? Vì sao?
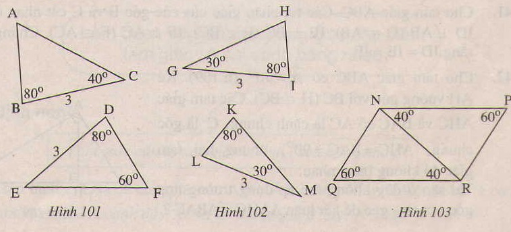

Tính các góc còn lại trên mỗi hình trên ta được:
\(\widehat{A}\)=600,\(\widehat{H}\)=700,\(\widehat{E}\)=400
\(\widehat{L}\)=700,\(\widehat{RNQ}\)=800,\(\widehat{RNP}\)= 800
Ta được: ∆ABC và ∆FDE(g. c.g)
Advertisements (Quảng cáo)
Vì \(\widehat{B}\) = \(\widehat{D}\)
BC=DE
\(\widehat{C}\)=\(\widehat{E}\)
∆NQR= ∆RPN(g.c .g)
Vì \(\widehat{RNQ}\)=\(\widehat{RNP}\)(=800)
NR là cạnh chung.
\(\widehat{NRP}\)=\(\widehat{RNP}\)(400)
