Bài 39. Trên mỗi hình 105,106,108 các tam giác vuông nào bằng nhau? Vì sao?. Bài 39 trang 124 – Sách giáo khoa toán 7 tập 1 – Trường hợp bằng nhau thứ ba của tam giác góc – cạnh – góc (G.C.G)
Advertisements (Quảng cáo)
Bài 39. Trên mỗi hình 105,106,108 các tam giác vuông nào bằng nhau? Vì sao?
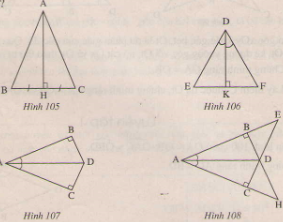
Hình 105
∆ABHvà ∆ACH có:
BH=CH(gt)
\(\widehat{AHB}\)=\(\widehat{AHC}\)(góc vuông)
AH là cạnh chung.
vậy ∆ABH=∆ACH(g.c.g)
Hình 106
∆DKE và ∆DKF có:
\(\widehat{EDK}\)=\(\widehat{FDK}\)(gt)
DK là cạnh chung.
Advertisements (Quảng cáo)
\(\widehat{DKE}\)=\(\widehat{DKF}\)(góc vuông)
Vậy ∆DKE=∆DKF(g.c.g)
Hình 107
Ta có:
∆ABD=∆ACD(g.c.g)
(Cạnh huyền góc nhọn).
Hình 108
Ta có:
∆ABD=∆ACD(Cạnh huyền – góc nhọn)
∆DBE=∆ACH(g.c.g)
∆ABH=ACE (g.c.g)